Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

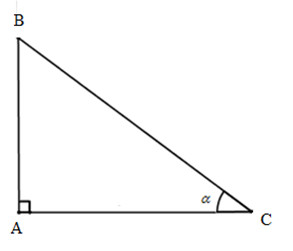
Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế:
sinC>0;cosC>0;tanC>0;cotC>0sinC>0;cosC>0;tanC>0;cotC>0
Vì hai góc B và C phụ nhau nên sinC = cosB = 0,8.
Ta có:
Sin2C+cos2C=1Sin2C+cos2C=1
⇒cos2C=1−sin2C=1−(0,8)2=0,36⇒cos2C=1−sin2C=1−(0,8)2=0,36
⇒cosC=0,6;⇒cosC=0,6;
tgC=sinCcosC=0,80,6=43;tgC=sinCcosC=0,80,6=43;
cotgC=cosCsinC=0,60,8=34

cosB=0,8=4/5 => BA=4 , BC=5
Áp dụng định lý Pytago trong tam giác vuông ABC, có:
AC2=BC2-BA2
(=) AC2=52-42=9
(=) AC=3
Ta có:
sinC=BA/BC=4/5
cosC=AC/BC=3/5
tanC=BA/AC=4/3
cotC=AC/BA=3/4
\(sin^2B+cos^2B=1\Leftrightarrow sin^2B-1-\left(0,8\right)^2=0.36.\Leftrightarrow sinB=0,6.\\\)
\(tanB=\frac{sinB}{cosB}=\frac{0,6}{0,8}=\frac{3}{4}\)
\(cotB=\frac{1}{tanB}=\frac{1}{\frac{3}{4}}=\frac{4}{3}.\)

neu ai tra loi dung cho minh trong may tieng nay to k cho1 nink

a) Ta có: \(cos\alpha=\dfrac{12}{13}\)
Mà: \(sin^2\alpha+cos^2a=1\)
\(\Rightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Rightarrow sin^2\alpha=1-\left(\dfrac{12}{13}\right)^2\)
\(\Rightarrow sin^2\alpha=\dfrac{25}{169}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{25}{169}}\)
\(\Rightarrow sin\alpha=\dfrac{5}{13}\)
Mà: \(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\dfrac{5}{13}}{\dfrac{12}{13}}=\dfrac{5}{12}\)
b) Ta có: \(cos\alpha=\dfrac{3}{5}\)
Mà: \(sin^2\alpha+cos^2\alpha=1\)
\(\Rightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Rightarrow sin^2\alpha=1-\left(\dfrac{3}{5}\right)^2\)
\(\Rightarrow sin^2\alpha=\dfrac{16}{25}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{16}{25}}=\dfrac{4}{5}\)
Mà: \(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\dfrac{4}{5}}{\dfrac{3}{5}}=\dfrac{4}{3}\)
2:
a: BC=căn 16^2+12^2=20cm
Xét ΔABC vuông tại A có
sin B=cos C=AC/BC=3/5
cos B=sin C=AB/BC=4/5
tan B=cot C=3/5:4/5=3/4
cot B=tan C=1:3/4=4/3
b: AH=căn 13^2-5^2=12cm
Xét ΔAHC vuông tại H có
sin C=AH/AC=12/13
=>cos B=12/13
cos C=HC/AC=5/13
=>sin B=5/13
tan C=12/13:5/13=12/5
=>cot B=12/5
tan B=cot C=1:12/5=5/12
c: BC=3+4=7cm
AB=căn BH*BC=2*căn 7(cm)
AC=căn CH*BC=căn 21(cm)
Xét ΔABC vuông tại A có
sin B=cos C=AC/BC=căn 21/7
sin C=cos B=AB/BC=2/căn 7
tan B=cot C=căn 21/7:2/căn 7=1/2*căn 21
cot B=tan C=1/căn 21/2=2/căn 21

Xét ΔABC vuông tại A có
\(sinB=sin56\simeq0,83\)
\(cosB=cos56\simeq0,56\)
\(tanB=tan56\simeq1,48\)
\(cotB=cot56\simeq0,67\)
Xét ΔABC vuông tại A có
\(cosC=sinB\simeq0,83\)
\(sinC=cosB\simeq-0,56\)
\(cotC=tanB=tan56\simeq1,48\)
\(tanC=cotB\simeq0,67\)

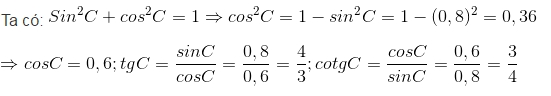
Xét ΔABC vuông tại A có \(\widehat{B}+\widehat{C}=90^0\)
nên \(sinB=cosC=\dfrac{4}{5}\)
\(sin^2B+cos^2B=1\)
=>\(cos^2B=1-\left(\dfrac{4}{5}\right)^2=\dfrac{9}{25}=\left(\dfrac{3}{5}\right)^2\)
=>\(cosB=\dfrac{3}{5}\)
\(tanB=\dfrac{sinB}{cosB}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotB=\dfrac{1}{tanB}=\dfrac{3}{4}\)
Vì tam giác ABC vuông tại A
Nên: \(\widehat{B}+\widehat{C}=90^o\\ \Rightarrow0^o< \widehat{C}< 90^o\)
\(\Rightarrow0< \sin C< 1\)
Ta có: \(\sin^2C+\cos^2C=1\Rightarrow\sin^2C=1-\left(\dfrac{4}{5}\right)^2=\dfrac{9}{25}\\ \Rightarrow\sin C=\dfrac{3}{5}\)
Lại có: \(\tan C=\dfrac{\sin C}{\cos C}=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\dfrac{3}{4}\\ \cot C=\dfrac{1}{\tan C}=\dfrac{4}{3}\)