Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMEN có
góc AME=gócANE=góc MAN=90 độ
nên AMEN là hình chữ nhật
b: \(AB=\sqrt{10^2-6^2}=8\left(cm\right)\)
Xét ΔCAB có NE//AB
nên NE/AB=CE/CB=1/2
=>NE=4cm
Xét ΔBAC có ME//AC
nên ME/AC=BE/BC=1/2
=>ME=3cm
=>SAMEN=4*3=12cm2

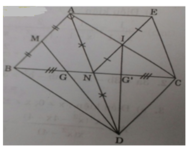
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)

a: Xét tứ giác AEGF có
\(\widehat{AEG}=\widehat{AFG}=\widehat{FAE}=90^0\)
=>AEGF là hình chữ nhật
b: Ta có: GF\(\perp\)AC
AB\(\perp\)AC
Do đó: GF//AB
Ta có: GF//AB
E\(\in\)BA
I\(\in\)FG
Do đó: EB//FI
Xét tứ giác BEIF có
BE//IF
BF//EI
Do đó: BEIF là hình bình hành
c: Xét ΔABC có
G là trung điểm của BC
GE//AC
Do đó: E là trung điểm của AB
=>AE=EB(2)
Xét ΔABC có
G là trung điểm của BC
GF//AB
Do đó: F là trung điểm của AC
Ta có: AEGF là hình chữ nhật
=>AE=GF(1)
Ta có: BEIF là hình bình hành
=>FI=EB(3)
Từ (1),(2),(3) suy ra GF=FI
=>F là trung điểm của GI
Xét tứ giác AGCI có
F là trung điểm chung của AC và GI
=>AGCI là hình bình hành
Hình bình hành AGCI có AC\(\perp\)GI
nên AGCI là hình thoi

Xét tam giác ABC có EA=EB ;MB=MC
suy ra ME là đường trung bình cũa tam giác ABC
suy ra ME // AC hay gócAEM=900 (1)
Tương tự góc MFA=900 (2)
góc EAF=900 (3)
từ (1) ;(2) ;(3) suy ra AEMF là hình chữ nhật

a: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: \(AE=\dfrac{AB}{2}=\dfrac{4}{2}=2\left(cm\right)\)
AF=AC/2=3cm
Do đó: \(S_{AEMF}=2\cdot3=6\left(cm^2\right)\)
c: Xét ΔCAB có
M là trung điểm của BC
MF//AB
Do đó F là trung điểm của AC
Xét tứ giác AMCK có
F là trung điểm chung của AC và MK
nên AMCK là hình bình hành
mà MA=MC
nên AMCK là hình thoi

a: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
b: \(AE=\dfrac{AB}{2}=\dfrac{4}{2}=2\left(cm\right)\)
AF=AC/2=3cm
Do đó: \(S_{AEMF}=2\cdot3=6\left(cm^2\right)\)
c: Xét ΔCAB có
M là trung điểm của BC
MF//AB
Do đó F là trung điểm của AC
Xét tứ giác AMCK có
F là trung điểm chung của AC và MK
nên AMCK là hình bình hành
mà MA=MC
nên AMCK là hình thoi

a: BC=10cm
AM=5cm
b: Xét tứ giác AEMF có góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
c: Xét ΔCAB có
M là trung điểm của BC
MF//AB
Do đó F là trung điểm của AC
Xét tứ giác AMCD có
F là trung điểm chung của AC và MD
nên AMCD là hình bình hành
mà MA=MC
nên AMCD là hình thoi