Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Cho tam giác ABC vuông tại A đường cao AH, biết AB = 3cm; AC = 4 cm tính: a) BC,AH,HB b) số đo góc B

a) Áp dụng định lí Py - ta - go vào tam giác vuông ABC ta có:
BC = \(\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}\)
BC = 5 cm
Từ hệ thức của cạnh góc vuông và hình chiếu của nó trên cạnh huyền suy ra:
HB = \(\dfrac{AB^2}{BC}=\dfrac{3^2}{5}=1,8\) cm
Ta có: HB + HC = BC
1,8 + HC = 5
HC = 3,2 cm
Theo hệ thức liên quan đến đường cao ta có:
AH2 = HB . HC
AH2 = 1,8 . 3,2
AH2 = 5,76
⇒ AH = 2,4 cm

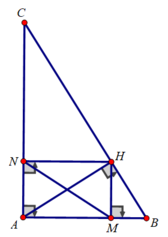
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

a,Sin B=\(\frac{AC}{BC}=\)\(\frac{4}{5}=0.8\)
Cos B=\(\frac{AB}{BC}=\frac{3}{5}=0,6\)
Tan B =\(\frac{AC}{AB}=\frac{4}{3}\)
Cot B=\(\frac{AB}{AC}=\frac{3}{4}=0,75\)
b,Vì sin B = 0,8 => B=53o
=> C=37o(áp dụng hệ quả định lí tổng r tính)

b) Xét tam giác AHB vuông tại H, HM là đường cao có:

∠(AMN) + ∠(ANM ) = 90 0 ⇒ ∠(ANM ) = 90 0 - ∠(AMN) = 53 , 1 0
Áp dụng định lý Py-ta-go vào tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Ta có:
\(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^o\)
Mà: \(\widehat{B}+\widehat{C}=90^o\Rightarrow\widehat{C}=90^o-53^o=37^o\)
Vậy: ...
\(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\left(Pytago\right)\)
\(=3^2+4^2\)
\(=25\)
\(\Rightarrow BC=5\left(cm\right)\)
\(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\simeq53^0\)
\(\Rightarrow\widehat{C}\simeq90^0-53^0=37^0\)