Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{BM}=\dfrac{4}{6}=\dfrac{2}{3}\)
b: Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\left(1\right)\)
Xét ΔAMC có
ME là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)
Ta có: M là trung điểm của BC
nên MB=MC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
c: Xét ΔABC có
\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC
a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
góc C chung
=>ΔHAC đồng dạng vói ΔABC
b: \(AB=\sqrt{5^2-3^2}=4\left(cm\right)\)
AH=3*4/5=2,4cm
HB=4^2/5=3,2cm
c: FH/FA=BH/BA
EA/EC=BA/BC
BH/BA=BA/BC
=>FH/FA=EA/EC
Theo t/c đường phân giác, ta được: \(\frac{BD}{BA}=\frac{DF}{AF},\frac{BA}{BC}=\frac{EA}{EC}\)
Chứng minh được \(\Delta BAC\infty\Delta BDA\left(g.g\right)\Rightarrow\frac{BA}{BC}=\frac{BD}{BA}\)
Vậy \(\frac{DF}{FA}=\frac{AE}{EC}\)
Bạn nên suy nghĩ một lúc nếu ko làm được thì mới hỏi. Chúc bạn học tốt.
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
Xét ΔHAC vuông tại H và ΔABC vuông tại A có
góc C chung
=>ΔHAC đồng dạng với ΔABC
=>ΔHBA đồng dạng với ΔHAC
b: BC=căn 6^2+8^2=10cm
AH=6*8/10=4,8cm
d: ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
`a,15x-8x=9`
`<=>7x=9`
`<=>x=9/7`
`b,(x+3)(x-5)=0`
`<=>` $\left[ \begin{array}{l}x+3=0\\x-5=0\end{array} \right.$
`<=>` $\left[ \begin{array}{l}x=5\\x=-3\end{array} \right.$
Vậy `S={-3,5}`
Bài 2:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
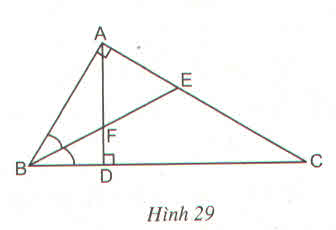
a: Xét ΔDBA vuông tại D và ΔABC vuông tại A có
góc ABC chung
Do đó: ΔDBA\(\sim\)ΔABC
Suy ra: DB/AB=AB/BC(1)
b: Xét ΔBDA có BFlà phân giác
nên DF/FA=DB/AB(2)
Xét ΔABC có BE là phân giác
nên AE/EC=BA/BC(3)
Từ (1), (2) và (3) suy ra DF/FA=AE/EC