Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

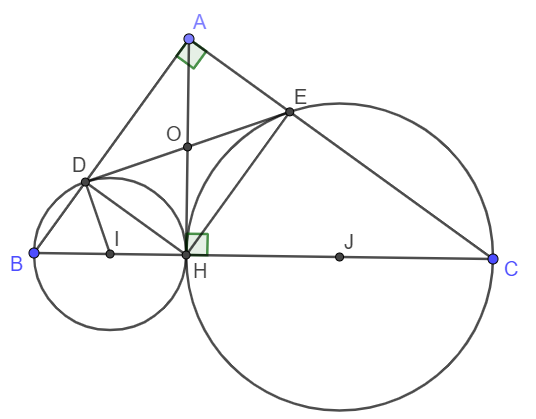
Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chỉ cần chứng minh ID\perp DEID⊥DE .
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có: \widehat{BDH}=\widehat{CEH}=90^oBDH=CEH=90o.
Suy ra tứ giác ADHE là hình chữ nhật.
Gọi O là giao điểm của AH và DE, khi đó ta có OD = OH = OE = OA.
Suy ra tam giác ODH cân tại O vì vậy \widehat{ODH}=\widehat{OHD}ODH=OHD.
Ta cũng có tam giác IDH cân tại I suy ra \widehat{IDH}=\widehat{IHO}IDH=IHO.
Suy ra \widehat{IDO}+\widehat{OHD}=\widehat{IHD}+\widehat{IHA}=90^oIDO+OHD=IHD+IHA=90o \Leftrightarrow\widehat{IDO}=90^o⇔IDO=90o hay DI \perp⊥ DE.
Ta có DI\perp DE\left(D\in\left(I\right)\right)DI⊥DE(D∈(I)) suy ra DE tiếp xúc với (I) tại D.
Chứng minh tương tự ta cũng có DE tiếp xúc với (J) tại E.
Vậy DE là tiếp tuyến chung của đường tròn (I) và đường tròn (J).
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có : góc BHD = góc CEH=90°
=> tứ giác ADHE là hình chữ nhật
Gọi O là giao điểm của AH và DE khi đó ta có OD=OE=OA
=> Tam giác ODH cân tại O vì vậy góc ODH = góc OHD
Ta cũng có tam giác IDH cân tại I suy ra góc IDH= góc IHO
=> góc IDO + góc OHD = góc IHD + góc IHA=90° <=> góc IDO = 90° hay DI ⊥ DE
ta có DI ⊥ DE ( D ∈ I) => DE tiếp xúc với (I) tại D
Ta có DE tiếp xúc với (J) tại E
Vậy DE là tiếp tuyến chung của đường tròn (I) và đường tròn (J)
\perp \perp⊥\perp⊥\per⊥\perp⊥

a:
Xét đường tròn đường kính HB có
ΔHMB nội tiếp đường tròn
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét đường tròn đường kính HC có
ΔHNC nội tiếp đường tròn
HC là đường kính
Do đó: ΔHNC vuông tại N
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
nên AMHN là hình chữ nhật
b: \(BC=\sqrt{6^2+8^2}=10\)(cm)
=>AH=6*8/10=4,8(cm)
=>MN=4,8(cm)
c: góc IMN=góc IMH+góc NMH
=góc IHM+góc NAH
=góc HAC+góc HCA=90 độ
=>MN là tiếp tuyến của (I)
góc KNM=góc KNH+góc MNH
=góc KHN+góc MAH
=góc BAH+góc HBA=90 độ
=>MN là tiếp tuyến của (K)

Tam giác MBH nội tiếp đường tròn tâm I đường kính BH
=> Tam giác MHB vuông tại M => MH vg AB => AMH = 90 độ
Tam giác HNC nội tiếp đường tròn tâm O đk HC => Tam giác NHC vuông tại N
=> ANH = 90 độ
TG NAMH có ANH = HMA = MAN = 90 độ
=> NAMH là HCN . Gọi MN giao AH tại O => OM = OH ; ON = OH ( tính chất HCN)
Tam giác BMH vuông tại M có MI là trung tuyến => MI = IH = 1/2 BH => Tam giác IMH cân tại I
=> IMH = IHM (1)
Tam giác OMH có OM = OH => tam giác OMH cân tại O => OMH = OHM (2)
Từ (1) và (2) => IMH + OMH = IHM + OHM => OMI = IHO = 90 độ
=> MN vg IM
=> MN là tiếp tuyến đường tròn tâm I (*)
CM tương tự MN vg NK => MN là tiếp tuyến đường tròn tâm K (**)
Từ (*) và(**) => MN là tiếp tuyến chung của đường tròn tâm I và K

a: Xét (I) có
ΔHDB nội tiếp
HB là đường kính
Do đo: ΔHDB vuông tại D
Xét (K) có
ΔCHE nội tiếp
CH là đường kính
DO đó: ΔCHE vuông tại E
Xét tứ giác AEHD có
góc AEH=góc ADH=góc DAE=90 độ
nên AEHD là hình chữ nhật
b: BC=10cm
=>AH=6*8/10=4.8cm
=>DE=AH=4,8cm
c: góc IDE=góc IDH+góc EDH
=góc IHD+góc EAH
=90 độ
=>DI vuông góc với DE
=>DE là tiếp tuyến của (I)
góc KED=góc KEH+góc DEH
=góc KHE+góc DAH
=90 độ
=>ED là tiếp tuyến của (K)

a: O là trung điểm của BC
b: Xét \(\left(\dfrac{BH}{2}\right)\) có
ΔBDH là tam giác nội tiếp
BH là đường kính
Do đó: ΔBDH vuông tại D
Xét \(\left(\dfrac{CH}{2}\right)\)có
ΔCHE nội tiếp đường tròn
CH là đường kính
Do đó: ΔCHE vuông tại E
Xét tứ giác ADHE có
\(\widehat{AEH}=\widehat{ADH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật