Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B A C M D 1 2
1)A)XÉT \(\Delta ABM\)VÀ\(\Delta DCM\)CÓ
\(BM=CM\left(GT\right)\)
\(\widehat{M_1}=\widehat{M_2}\left(Đ/Đ\right)\)
\(AM=DM\left(GT\right)\)
\(\Rightarrow\Delta ABM=\Delta DCM\left(C-G-C\right)\)
\(\Rightarrow AB=CD\)(HAI CẠNH TƯƠNG ỨNG)(1)
TA CÓ XÉT \(\Delta ABC\)VUÔNG TẠI B
\(\Rightarrow\widehat{B}>\widehat{C};\widehat{B}>\widehat{A}\)
VÌ\(\widehat{B}>\widehat{C}\)
\(\Rightarrow AB< AC\)QUAN HỆ GIỮA GÓC VÀ CẠNH ĐỐI DIỆN(2)
TỪ (1) VÀ (2) => \(AC>CD\)
B) CÂU B QUAN HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN
b) XÉT \(\Delta ADC\)
CÓ \(DC< AC\left(CMT\right)\)
\(\Rightarrow\widehat{ADC}>\widehat{DAC}\left(1\right)\)QUA HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN
MÀ \(\Delta ABM=\Delta DCM\left(CMT\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{MDC}\)
HAY\(\widehat{BAM}=\widehat{ADC}\left(2\right)\)
TỪ (1) VÀ (2) \(\Rightarrow\widehat{BMA}>\widehat{MAC}\)

a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AB=CD và AB//CD
b: Sửa đề: AB<AC
AB=CD
=>CD<AC
=>góc CAD<góc CDA
=>góc CAD<góc BAD
c: góc AMB=góc MAC+góc ACB
góc AMC=góc MAB+góc ABC
mà góc MAC<góc MAB và góc ACB<góc ABC
nên góc AMB<góc AMC

Bạn tự vẽ hình nha![]()
a.
Xét tam giác MBE và tam giác MCA có:
MB = CM (AM là trung tuyến của tam giác ABC => M là trung điểm của BC)
BME = CMA (2 góc đối đỉnh)
AM = EM (gt)
=> Tam giác MBE = Tam giác MCA (c.g.c)
=> BE = CA (2 cạnh tương ứng)
=> MEB = MAC (2 góc tương ứng)
mà 2 góc này ở vị trsi so le trong
=> BE // AC
b.
BE // AC (theo câu a)
=> AFD = BED (2 góc so le trong)
Xét tam giác DFA và tam giác DEB có:
AFD = BED (chứng minh trên)
DF = DE (gt)
FDA = EDB (2 góc đối đỉnh)
=> Tam giác DFA = Tam giác DEB (g.c.g)
=> FA = EB (2 cạnh tương ứng)
mà EB = AC (theo câu a)
=> FA = AC
=> A là trung điểm của FC
c.
Tam giác ABC có:
AB < AC (gt)
mà AC = EB (theo câu a)
=> AB < EB
=> BEM < BAM (quan hệ giữa góc và cạnh đối diện trong tam giác)
mà BEM = CAM (tam giác MBE = tam giác MCA)
=> CAM < BAM
Chúc bạn học tốt![]()
Phương An giúp mình làm bài hình còn lai được không?
đề nè
cho góc nhọn xOy; trên tia Ox lấy A(A#O); trên tia Oy lấy điểm B (B # O)sao cho OA = OB; kẻ ACvuông góc với OY (CE Oy) ; BD vuông góc Ox ( D E Ox); I là giao diểm của AC và BD
a. chứng minh tam giác AOC= tam giác BOD
b. So sánh IC và IA
c. Chứng minh tam giác AIB cân
d. Chứng minh góc IAB=M góc 1\2 góc AOB
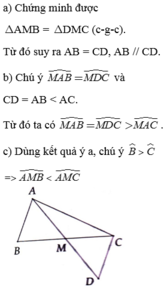
1: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: CD=AB
mà AB<AC
nên CD<AC
2: Ta có: \(\widehat{BAM}=\widehat{CDA}\)
mà \(\widehat{CDA}>\widehat{MAC}\left(AC>MC\right)\)
nên \(\widehat{BAM}>\widehat{CAM}\)