Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo lời giải tại đây:
https://hoc24.vn/cau-hoi/cho-tam-giac-abc-vuong-o-a-duong-cao-ah-phan-giac-ad-goi-i-j-lan-luot-la-cac-giao-diem-cac-duong-phan-giac-cua-tam-giac-abh-ach-e-la-giao-diem-c.8915069447339

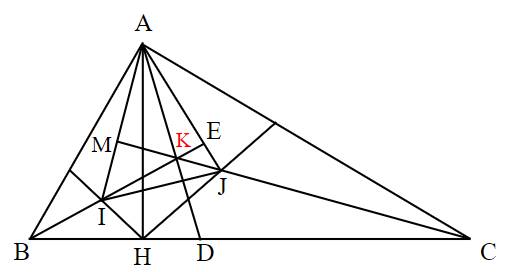
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC
^EAC+^BAE=^BAC=900. Mà ^EBA=^EAC => ^EBA+^BAE=900.
Xét tam giác ABE: ^EBA+^BAE=900 => ^AEB=900.
=> Tam giác ABE vuông tại E (đpcm)
b) Gọi M là giao điểm của CJ và AI.
Gọi K là giao điểm của BE và CM.
^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM
^MAB+^MAC=900 => ^ACM+^MAC=900 => Tam giác AMC vuông tại M.
Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.
=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.
Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.
BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.
=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)

A B C D H I J E K M
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC
^EAC+^BAE=^BAC=900. Mà ^EBA=^EAC => ^EBA+^BAE=900.
Xét tam giác ABE: ^EBA+^BAE=900 => ^AEB=900.
=> Tam giác ABE vuông tại E (đpcm)
b) Gọi M là giao điểm của CJ và AI.
Gọi K là giao điểm của BE và CM.
^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM
^MAB+^MAC=900 => ^ACM+^MAC=900 => Tam giác AMC vuông tại M.
Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.
=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.
Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.
BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.
=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)
a) Ta có: ^ABH=^HAC (Cùng phụ với ^BAH) => 1/2^ABH=1/2^HAC => ^EBA=^EAC
^EAC+^BAE=^BAC=900
. Mà ^EBA=^EAC => ^EBA+^BAE=900
.
Xét tam giác ABE: ^EBA+^BAE=900
=> ^AEB=900
.
=> Tam giác ABE vuông tại E (đpcm)
b) Gọi M là giao điểm của CJ và AI.
Gọi K là giao điểm của BE và CM.
^ACH=^BAH (Cùng phụ với ^HAC) => 1/2^ACH=1/2^BAH => ^MAB=^ACM
^MAB+^MAC=900
=> ^ACM+^MAC=900
=> Tam giác AMC vuông tại M.
Xét tam giác AIJ: IE vuông góc AJ, JM vuông góc AI. Mà IE giao JM tại K.
=> K là trực tâm của tam giác AIJ => AK vuông góc IJ.
Xét tam giác ABC: BE là phân giác ^ABC, CM là phân giác ^ACB.
BE giac CM tại K => AK là phân giác ^BAC. Mà AD là phân giác ^BAC.
=> A,K,D thẳng hàng => AD vuông góc với IJ (đpcm)
gọi F là gia điểm của AI và AJ; M là giao điểm của AI và BC; N là giao điểm của AJ và BC
ta có: AN là tia phân giác của nên = (1)
mà + = ; +=(2)
(1)(2) = tam giác ABN cân tại B BF là đường phân giác đồng thời là đường cao ứng với cạnh AN
BF vuông góc với AN
chứng minh tương tự: += ; += ; AM là tia phân giác của nên =
từ những điều trên ta có = tam giác AMC cân tại C CE là đường phân giác đồng thời là đường cao ứng với cạnh AM CE vuông góc với AM
tam giác ABC có 3 đường phân giác BF,CE,AD nên BF,CE,AD phải đồng quy tại 1 điểm (ta gọi điểm đó là K) (theo tính chất 3 đường phân giác trong một tam giác)
đúng không các pạn !!!
chuẩn rồi đó. biết làm rồi mà sao còn phai hỏi vậy