Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(CD=x,BC=y\left(x,y>0\right)\)
Ta có \(AB=\sqrt{BD^2-AD^2}=12\)
Ta có hệ phương trình: \(\hept{\begin{cases}\frac{x}{y}=\frac{AD}{AB}=\frac{4}{12}=\frac{1}{3}\\12^2+\left(4+x\right)^2=y^2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=3x\\144+\left(4+x\right)^2=\left(3x\right)^2\end{cases}}\Leftrightarrow\hept{\begin{cases}y=3x\\x=5\left(h\right)x=-4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=5\\y=15\end{cases}}\)(Vì \(x,y>0\))
Vậy \(S_{ABC}=\frac{AB.\left(AD+CD\right)}{2}=\frac{12.\left(4+5\right)}{2}=54.\)

Theo t/c đường phân giác: AD/AB = ID/IB = 1/2 --> ID = 1/2AB
Mà AD² + AB² = BD² = 15².5 hay 1/4AB² + AB² = 15².5 --> AB = 30 --> AD = 15
Lại theo t/c đường phân giác: AD/DC = AB/BC --> DC/BC = AD/AB = 1/2
--> BC = 2DC
Theo đ/l Pytago AB² + AC² = BC² hay 30² + (DC + 15)² = 4DC²
<=> DC² - 10DC - 375= 0 --> DC = 25 (loại nghiệm -15)
--> AC = AD + DC = 15 + 25 = 40
--> S(ABC) = 1/2AB.AC = 35 cm²
Đọc dòng đầu thấy sai sai bạn ạ
AD/AB=ID/IB=1/2 =>ID=1/2 IB chứ ko phải AB

Lời giải:
Theo tính chất tia phân giác:
$\frac{AB}{BC}=\frac{AD}{DC}=\frac{4\sqrt{10}}{5\sqrt{10}}=\frac{4}{5}$
$AC=4\sqrt{10}+5\sqrt{10}=9\sqrt{10}$
Áp dụng định lý Viet:
$BC^2=AB^2+AC^2$
$\Leftrightarrow (\frac{5}{4}AB)^2=AB^2+(9\sqrt{10})^2$
$\Leftrightarrow AB^2=1440$
$BD=\sqrt{AB^2+AD^2}=\sqrt{1440+(4\sqrt{10})^2}=\sqrt{1440+160}=40$ (cm)

=) Áp dụng liên tục py-ta-go và định lí đường phân giác quá dễ đó bạn :V
\(\frac{AD}{AB}=\frac{ID}{IB}=\frac{1}{2}vs.AD^2+AB^2=\left(6\sqrt{3}+3\sqrt{3}\right)^2=...\\
\)
Tìm đ.c AD và AB
Làm tươn tự trên đối với tg ABC
\(\frac{AD}{DC}=\frac{AB}{BC}vs.AB^2+\left(AD+DC\right)^2=BC^2.\\
\)
\(Chỉ-cần-giải-hệ-là-ra-....\\
\)

a, \(vì\)AD là phân giác suy ra góc BAD =góc DAC =45 ĐỘ
cos45 độ = AD/AB =4 /AB =1/ căn 2 suy ra AB =4 NHÂN CĂN 2
TH TỰ dùng sin 45 độ =dc/ac =5/ad =1/căn 2 suy ra AC =5 CĂN 2 ÁP DỤNG PITA GO TÌM RA CẠNH bc
b,

Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow AB^2=BD^2-AD^2=\left(\sqrt{10}\right)^2-1^2=9\)
hay AB=3(cm)
Xét ΔABD vuông tại A có
\(\sin\widehat{ABD}=\dfrac{AD}{BD}=\dfrac{1}{\sqrt{10}}\)
nên \(\widehat{ABD}\simeq18^026'\)
mà \(\widehat{ABC}=2\cdot\widehat{ABD}\)(BD là tia phân giác của \(\widehat{ABC}\))
nên \(\widehat{ABC}\simeq2\cdot18^026'=36^052'\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\cos\widehat{ABC}\)
\(\Leftrightarrow BC=\dfrac{AB}{\cos\widehat{ABC}}=\dfrac{3}{\cos36^052'}\)
hay \(BC\simeq3.75cm\)
Vậy: \(BC\simeq3.75cm\)

Cho tam giác ABC vuông tại A,phân giác AD
a,CM √2AD =1AB +1AC
b, Gọi I là giao điểm các đường phân giác của tam giác ABC, biết IB=√5,IC=√10. Tính diện tích tam giác ABC
a) Đặt AB = c; AC = b; AD = d.
Áp dụng công thức tính diện tích tam giác bằng ½ tích hai cạnh nhân sin góc xen giữa ta có:
S ABD = ½.AB.AD.sin BAD = ½.cd.sin 45º = ½cd.1/√2
Tương tự: S ACD = ½bd.1/√2
=> S ABC = S ABD + S ACD = ½cd.1/√2 + ½bd.1/√2 = ½d(b + c)/√2
mà S ABC = ½bc
=> ½d(b + c)/√2 = ½bc
=> (b + c)/bc = √2/d
<=> 1/b + 1/c = √2/d
b,Kẻ CH ⊥ BI và CH cắt BA tại K. Tam giác BCK có BH vừa là phân giác vừa là đường cao Tam giác BCK cân tại B => BH là đường trung tuyến => CH = KH. và KC = 2HC.
Đặt BC = x Ta có: AD = BK - AB = BC - AB = x - AB
Gọi giao điểm của AC và BH là E.
Xét tam giác AEB và tam giác HEC có góc EAB = góc EHC = 90độ và góc AEB = góc HEC (đối đỉnh)
tam giác AEB ~ tam giác HEC(g.g)
Góc HCE = góc ABE.
Góc HCE = góc ABC/2 (1)
Mà Góc ECI = gócACB/2 (2)
Từ (1) và (2) Góc ICH = Góc HCE + Góc ECI = (gócABC + góc ACB)/2 = 90độ/2 = 45độ.
Xét tam giác HIC có góc IHC = 90độ và Góc ICH = 45 độ (góc còn lại chắc chắn = 45 độ)
tam giác HIC vuông cân tại H => HI = HC.
Áp dụng đinh lý Py-ta-go cho tam giác này ta được: 2HI² = IC²
√2.IH = IC hay CH = IC/√2.
CH =HI=√10 /√2
Suy ra BH=HI+IB=√10 /√2+√5
=>BC=√((√10 /√2+√5)²+(√10 /√2)²)
KC = 2CH = 2.√10/√2
Xét tam giác: AKC có góc KAC = 90độ và Áp dụng định lý Py-ta-go ta có: KC² = AK² + AC²
AC² = KC² - AK² hay AC² = (2.√10/√2)² - (x - AB)² (3)
Tương tự đối với tam giác ABC ta có: AC² = BC² - AB² AC² = x² - AB² (4)
Từ (3) và (4) suy ra (2.√10/√2)² - (x - AB)² = x² - AB²
20 - (x² - 2ABx +AB²) = x² - AB²
=>10=x(x-AB)
sau đó tính AB rồi tính AC And S ABC

xét tam giác ABD có góc BAD=90 độ
= BD^2=AB^2+AD^2
=>AB^2=BD^2-AD^2=10-1=9
=> AB=3 cm
có AC=AD+DC=1+√10 cm
tam giác ABC vuông tại A
=>AB^2+AC^2=BC^2
=>BC^2=9+1+2√10+10=20+2√10
=>BC=√(20+2√10)
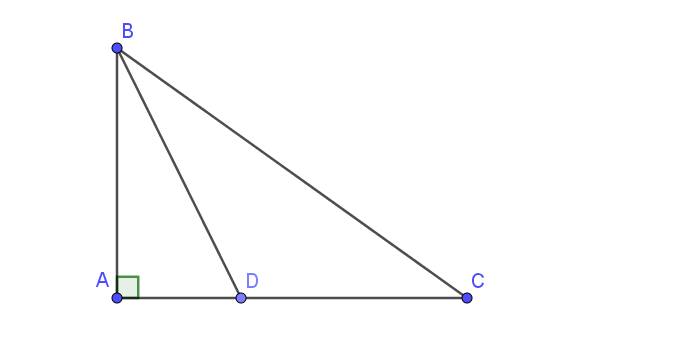
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow AB^2=BD^2-AD^2=\left(4\sqrt{10}\right)^2-4^2=144\)
hay AB=12(cm)
Xét ΔABD vuông tại A có
\(\tan\widehat{ABD}=\dfrac{AD}{AB}=\dfrac{4}{12}=\dfrac{1}{3}\)
hay \(\widehat{ABD}\simeq18^026'\)
mà \(\widehat{ABC}=2\cdot\widehat{ABD}\)(BD là tia phân giác của \(\widehat{ABC}\))
nên \(\widehat{ABC}\simeq36^052'\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan\widehat{ABC}\)
\(\Leftrightarrow AC=12\cdot\tan36^052'\simeq9\)(cm)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{12\cdot9}{2}=\dfrac{108}{2}=54\left(cm^2\right)\)