Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tam giác ALI và tam giác ALD có : AL chung
DL = LI (gt)
^ALD = ^ALI = 90
=> tam giác ALI = tam giác ALD (2cgv)
=> AI = AD
tương tự cm được tam giác AKD = tam giác AKJ (2cgv) => AJ = AD
=> AI = AJ
=> tam giác AIJ cân tại A

A C D B L I K J
a, xét tam giác ALI và tam giác ALD có : AL chung
DL = LI (gt)
^ALD = ^ALI = 90
=> tam giác ALI = tam giác ALD (2cgv)
=> AI = AD
tương tự cm được tam giác AKD = tam giác AKJ (2cgv) => AJ = AD
=> AI = AJ
=> tam giác AIJ cân tại A
a, Vì A thuộc đường trung trực của DI
nên AI = AD
Vì A thuộc đường trung trực của DJ nên AJ = AD
Do đó: AI=AJ hay \(\Delta\) AIJ cân tại A
b, ALI = ALD ( c.c.c )
=> AKD = AKJ ( c.c.c )
=> AIJ cân ( cmt )
=> DA là tia p/g của LDK

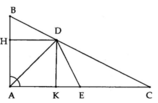

c) Do DH vuông góc với AB nên DH là khoảng cách từ D đến AB.
Tương tự DK là khoảng cách từ D đến AC.
Suy ra DH = DK. Suy ra điểm D cách đều AB và AC.