Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
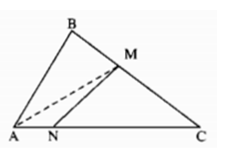
Kẻ đoạn thẳng AM. Xét tam giác MAC. Chứng minh tương tự như bài 1.4 ta có MN < a, trong đó a là đoạn lớn nhất trong hai đoạn thẳng MA và MC. Nếu ta chứng minh được
MA < AC và MC < AC thì sẽ suy ra được a < AC, từ đó có MN < AC.
Trong tam giác ABC có AB ≤ AC, M ∈ BC (M ≠ B, M ≠ C); Chứng minh tương tự bài 1.4, ta có AM < AC. Mặt khác MC < BC ≤ CA. Vậy a < AC, suy ra MN < AC.
bạn ơi cách này trong phần giải đằng sau sách bài tập toán 7 mà !!!

B A C M N
Áp dụng bất đẳng thức tam giác cho tam giác CMN ta có:
\(CN+CM>MN\)
Vì N nằm trên BC nên CN<BC
Vì M nằm trên AC nên CM<AC
=>\(BC+AC>CM+CN>MN\)
Đến đây tự giải tiếp thì dễ rồi

Hình :
A B C M
Ta có : \(\widehat{M}_1+\widehat{M}_2=180^o\) nên chỉ có hai khả năng xảy ra ứng với các vị rí của M trên BC là :
\(\widehat{M}_1>90^o\) hoặc \(\widehat{M}_2\ge90^o\)
* Nếu \(\widehat{M}_1>90^o\) thì tam giác AMC có góc M1 tù nên AM < AC .
* Nếu \(\widehat{M}_2\ge90^o\) thì trong tam giác ABM có AM < AB . Kết hợp với giả thiết AB < AC , ta suy ra AM < AC . Vậy ta luôn có AM < AC

Bạn tham khảo lời giải tại đây:
cho tam giác ABC , AB - Hoc24

A B C M Vì \(AB\le AC\) nên \(\widehat{ACB}\le\widehat{ABC}\) (quan hệ giữa cạnh và góc đối diện) (1)
Mà \(\widehat{AMC}=\widehat{ABC}+\widehat{BAM}\) (tính chất góc ngoài của tam giác) (2)
Từ (1) và (2) \(\Rightarrow\) \(\widehat{ACB}< \widehat{AMC}\)
\(\Rightarrow AM< AC\) (quan hệ giữa cạnh và góc đối diện)
Chúc bn học tốt!![]()
Sửa đề: AB>=AC
Ta có: \(\widehat{AMB}+\widehat{AMC}=180^0\)
nên \(\left[{}\begin{matrix}\widehat{AMB}>90^0\\\widehat{AMC}>=90^0\end{matrix}\right.\)
Nếu \(\widehat{AMC}>=90^0\) thì ΔAMC có cạnh AC là cạnh lớn nhất
nên AC>AM
Nếu \(\widehat{AMB}>90^0\) thì ΔABM có AB là cạnh lớn nhất
=>AB>AM
mà AB<AC
nên AM<AC