Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác ABC nhọn:
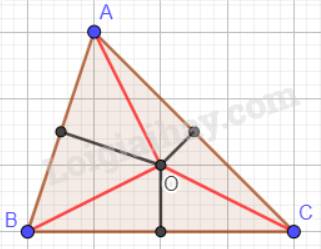
b) Tam giác ABC vuông tại A:
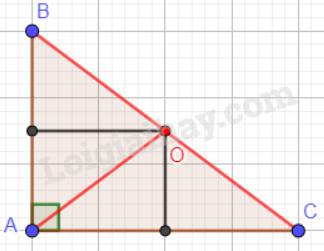
c) Tam giác ABC có góc A tù:
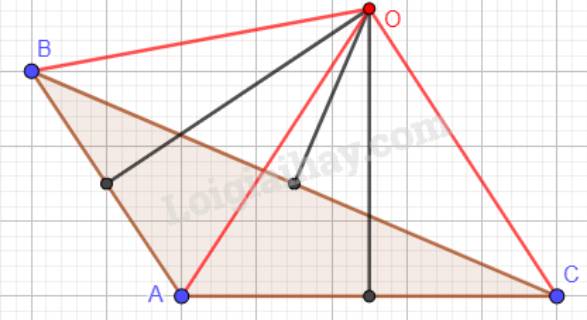

a: Vì góc A nhọn nên chắc chắn tam giác ABC không thể vuông cân
=> Loại
b: Gọi giao điểm của BH và AC là K
=> BK\(\perp\)AC tại K
Ta có: ΔABK vuông tại K
nên \(\widehat{ABK}+\widehat{BAK}=90^0\)
hay \(\widehat{BAC}=60^0\)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)
nên ΔABC đều

từ a kẻ đường thẳng song song với AM cắt AI tại O chứng minh tam giác OAN = ABC

a: Xét ΔAKB và ΔAKC có
AB=AC
góc BAK=góc CAK
AK chung
=>ΔAKB=ΔAKC
ΔABC cân tại A
mà AK là phân giác
nên AK vuông góc CB
b: Xét ΔACB có
BM,AK là trung tuyến
BM cắt AK tại G
=>G là trọng tâm
c: BK=CK=18/2=9cm
=>\(AK=\sqrt{30^2-9^2}=3\sqrt{91}\left(cm\right)\)
=>\(AG=2\sqrt{91}\left(cm\right)\)
a)
Nhận xét: H là một điểm nằm trong tam giác ABC.
b)
Nhận xét: H trùng với đỉnh A của tam giác ABC.
c)
Nhận xét: H nằm ngoài tam giác ABC.