K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PD
4


26 tháng 5 2017
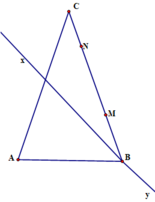
bn tự vẽ hình nhs!!!!
Hai tam giác BAE và CAE có chung đấy AE
Đường cao hạ từ đình B của tam giác BAE gấp đôi đường cao hạ từ đỉnh C của tam giác CAE
\(\Rightarrow\)BAE = 2. CAE
\(\Rightarrow\) Diện tích tam giác BAE nhỏ hơn diện tích tam giác CAE

12 tháng 2 2015
sao ko ai giải hết vậy nè thôi để mình giải luôn nha
Lấy các điểm A và B không
trùng O sao cho A thuộc tia Oa , B thuộc tia Ob. Tia Oc nằm giữa hai tia Oa, Ob nên cắt đoạn thẳng AB tại điểm C nằm giữa A và B. Cũng vậy, tia Om cắt đoạn AC tại điểm M nằm giữa A và C, tia On cắt đoạn CB tại N nằm giữa C và B. Tia Oc cắt đoạn MN tại C nằm giữa M và N nên tia Oc nằm giữa hai tia Om và On. ... còn lại tự giải nha
LS
9 tháng 12 2020
a.trên tia AB, lấy 3 điểm A,B,C thẳng hàng
AB>AC(8>4)
Nên C nằm giữa 2 điểm A và B
AC+CB=AB
4+CB=8
CB=8-4=4(cm)