Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(tự vẽ hình )
câu 4:
a) có AB2 + AC2 = 225
BC2 = 225
Pytago đảo => \(\Delta ABC\)vuông tại A
b) Xét \(\Delta MAB\)và \(\Delta MDC\)
MA = MD (gt)
BM = BC ( do M là trung điểm của BC )
\(\widehat{AMB}=\widehat{CMD}\)( hai góc đối đỉnh )
=> \(\Delta MAB\)= \(\Delta MDC\) (cgc)
c) vì \(\Delta MAB\)= \(\Delta MDC\)
=> \(\hept{\begin{cases}AB=DC\\\widehat{MAB}=\widehat{MDC}\end{cases}}\)
=> AB// DC
lại có AB \(\perp\)AC => DC \(\perp\)AC => \(\Delta KCD\)vuông tại C
Xét \(\Delta\) vuông ABK và \(\Delta\)vuông KCD:
AB =CD (cmt)
AK = KC ( do k là trung điểm của AC )
=> \(\Delta\)vuông AKB = \(\Delta\)vuông CKD (cc)
=> KB = KD
d. do KB = KD => \(\Delta KBD\)cân tại K
=> \(\widehat{KBD}=\widehat{KDB}\)(1)
có \(\Delta ADC\)vuông tại C => \(AD=\sqrt{AC^2+DC^2}=15\)
=> MD = 7.5
mà MB = 7.5
=> MB = MD
=> \(\Delta MBD\)cân tại M
=> \(\widehat{MBD}=\widehat{MDB}\)(2)
Từ (1) và (2) => \(\widehat{KBD}-\widehat{MBD}=\widehat{KDB}-\widehat{MDB}\)hay \(\widehat{KBM}=\widehat{KDM}\)
Xét \(\Delta KBI\)và \(\Delta KDN\)có:
\(\widehat{KBI}=\widehat{KDN}\)(cmt)
\(\widehat{KBD}\)chung
KD =KB (cmt)
=> \(\Delta KBI\)= \(\Delta KDN\)(gcg)
=> KN =KI
=. đpcm
câu 5:
a) Xét \(\Delta ABM\)và \(\Delta MDC\):
MA=MD(gt)
MB=MC (M là trung điểm của BC)
\(\widehat{BMA}=\widehat{DMC}\)( đối đỉnh )
=> \(\Delta BMA=\Delta CMD\)(cgc)
b) Xét \(\Delta\)vuông ABC
có AM là đường trung tuyến của tam giác
=> \(AM=\frac{1}{2}BC\)mà \(BM=MC=\frac{1}{2}BC\)(do M là trung điểm của BC )
=> AM = BM = MC
có MA =MD => AM = MD =MB =MC
=> BM +MC = AM +MD hay BC =AD
Xét \(\Delta BAC\)và \(\Delta DCA\)
AB =DC
AC chung
BC =DC
=> \(\Delta BAC\)= \(\Delta DCA\)(ccc)
c. Xét \(\Delta ABM\)
BM=AM
\(\widehat{ABM}\)= 600
=> đpcm

a) Xét △AMB và △DMC có:
MA=MD(gt)
BMA=CMD(đối đỉnh)
MB=MC(M: trđ BC)
\(\Rightarrow\)△AMB=△DMC(c.g.c)
b) Xét △BMD và △CMA có:
MB=MC(M: trđ BC)
BMD=CMA(đối đỉnh)
MA=MD(gt)
\(\Rightarrow\)△BMD=△CMA(c.g.c)
\(\Rightarrow\)DBM=MCA(2 góc tương ứng)
Mà 2 góc ở vị trí so le trong
\(\Rightarrow\)BD//AC
Ta có:
AB\(\perp\)AC
BD//AC
\(\Rightarrow\)AB\(\perp\)BD
\(\Rightarrow\)đpcm
c) Vì △AMB=△DMC
\(\Rightarrow\)BAM=MCD(2 góc tương ứng)
Mà hai góc ở vị trí so le trong
\(\Rightarrow\)AB//DC
Ta có:
AB//DC
AB\(\perp\)AC
\(\Rightarrow\)AC\(\perp\)DC
Xét △BAC và △DCA có:
AC: chung
BAC=DCA(=90o)
AB=DC(△AMB=△DMC)
\(\Rightarrow\)△BAC=△DCA(c.g.c)
\(\Rightarrow\)AD=BC(2 cạnh tương ứng)
Mà AM=1/2AD
\(\Rightarrow\)AM=1/2BC
\(\Rightarrow\)đpcm

b) ta có CD//BE
CFE = FEN ( so le trong )
mà FEN =FEC ( EF là tia phân giác )
nên CFE = FEC
nên tam giác CFE cân tại C
mà CK là đường cao , nên CK cũng là tia phân giác
ta có CD\\EB
CFE=FEN(số lẻ trong )
mà FEN=FEC(EF là tia phân giác)
CFE=FEC
nên tam giácCFE cân tại C
mà CK là đường cao , nên CK cũng là tia phân giác
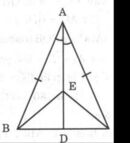




Ta có MD // AN suy ra A 1 ^ = M 1 ^ (cặp góc so le trong); ME // AC suy ra A 2 ^ = M 2 ^ (cặp góc so le trong).
Tia MA nằm giữa hai tia MD và ME. Do đó tia MA là tia phân giác của góc DME.
⇔ M 1 ^ = M 2 ^ ⇔ A 1 ^ = A 2 ^ ⇔ M là giao điểm của BC với tia phân giác của góc A
Ta có MD // AN suy ra A 1 ^ = M 1 ^ (cặp góc so le trong); ME // AC suy ra A 2 ^ = M 2 ^ (cặp góc so le trong).
Tia MA nằm giữa hai tia MD và ME. Do đó tia MA là tia phân giác của góc DME.
⇔ M 1 ^ = M 2 ^ ⇔ A 1 ^ = A 2 ^ ⇔ M là giao điểm của BC với tia phân giác của góc A