Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CD), BD cắt AM tại I. CMR 
a) Ta có: \(AD=\dfrac{1}{2}DC\)(gt)
mà \(EC=ED=\dfrac{DC}{2}\)(E là trung điểm của DC)
nên AD=EC=ED
b) Xét ΔCDB có
M là trung điểm của BC(gt)
E là trung điểm của CD(gt)
Do đó: ME là đường trung bình của ΔCDB(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//BD và \(ME=\dfrac{1}{2}BD\)(Định lí 2 về đường trung bình của tam giác)
hay ME//ID
Xét tứ giác MEDB có ME//BD(cmt)
nên MEDB là hình thang có hai đáy là ME và BD(Định nghĩa hình thang)
c) Xét ΔAME có
D là trung điểm của AE(AD=DE, D nằm giữa A và E)
DI//ME(cmt)
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
hay IA=IM(Đpcm)
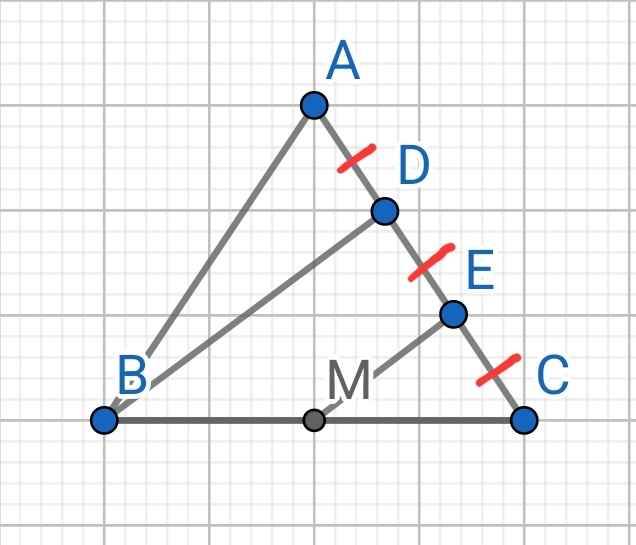
Sửa đề:
AD = DE = EC. BD cắt AM tại I
GIẢI
a) Sửa đề: Chứng mình BDEM là hình thang
Do DE = EC (gt)
⇒ E là trung điểm DC
Mà M là trung điểm BC (gt)
⇒ ME là đường trung bình của ∆BCD
⇒ ME // BD
Tứ giác BDEM có:
ME // BD (cmt)
⇒ BDEM là hình thang
b) Do AD = DE (gt)
⇒ D là trung điểm của AE
Do BD // ME (cmt)
⇒ BI // ME
Mà D là trung điểm của AE (cmt)
⇒ I là trung điểm của AM
⇒ IA = IM
a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.
Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.
Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.
Do đó DC // EM (tính chất đường trung bình).
b) Ta có D là trung điểm của AE (vì AD = DE, D ∈ AE).
Mà DI // EM (vì DC // EM).
Do đó DI là đường trung bình của tam giác AEM.
Suy ra I là trung điểm của AM.
b. Ta có: EM là đường trung bình của tam giác BDC => EM=1/2 DC
DI là đường trung bình của tam giác AEM=> DI=1/2EM
=> DI = 1/2. 1/2 DC = 1/4DC
=> IC = 3/4 DC
=> IC = 3DI
a. Xét tam giác BDC có E là TĐ BD, M là TĐ BC => ME là đường trung bình của tam giác BDC => ME//DC => ME//DI
Xét tam giác AEM có DI//ME và D là TĐ AE => I là TĐ AM => IA=IM