K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

27 tháng 3
Phần a: Tính góc DAE
Để tính góc \(\angle D A E\), ta cần sử dụng một số đặc điểm hình học của tam giác cân và các đường trung trực.
- Thông tin đã cho:
- Tam giác \(A B C\) là tam giác cân, nghĩa là \(A B = A C\).
- Góc \(\angle A = 110^{\circ}\).
- Các đường trung trực của \(A B\) và \(A C\) cắt nhau tại điểm \(F\), tạo ra các điểm \(D\) và \(E\) trên cạnh \(B C\).
- Các tính chất của các đường trung trực:
- Đường trung trực của một đoạn thẳng trong tam giác là đường vuông góc với đoạn thẳng đó và chia đoạn thẳng đó thành hai phần bằng nhau.
- Vì tam giác \(A B C\) là tam giác cân nên đường trung trực của \(A B\) và \(A C\) sẽ gặp nhau tại \(F\), tạo ra các góc vuông tại các điểm \(D\) và \(E\) trên cạnh \(B C\).
- Cách tính:
- \(F\) là trực tâm của tam giác \(A B C\), vì vậy \(\angle D A F = \angle E A F = 90^{\circ}\).
- Khi đó, góc \(\angle D A E = \angle D A F + \angle E A F\).
Vậy ta có thể tính:
\(\angle D A E = 90^{\circ} + 90^{\circ} = 180^{\circ} .\)
Phần b: Chứng minh \(\angle B A C = \angle B A E + 180^{\circ}\)
- Thông tin đã cho:
- Tam giác \(A B C\) là tam giác cân với \(A B = A C\).
- Góc \(\angle A = 110^{\circ}\).
- Các tính chất cần nhớ:
- Góc trong tam giác cân \(\triangle A B C\) có tính đối xứng.
- Góc \(\angle B A C\) là góc tại đỉnh của tam giác cân, và các đường trung trực chia góc này thành các góc phụ.
- Chứng minh:
- Vì \(\triangle A B C\) là tam giác cân, góc \(\angle A B C = \angle A C B\).
- Xét tam giác vuông \(\triangle A D F\) và \(\triangle A E F\) (vì \(A D \bot A B\) và \(A E \bot A C\)).
- Trong các tam giác này, ta có thể áp dụng các tính chất của góc vuông và các góc đối xứng.
\(\angle B A C = \angle B A E + 180^{\circ}\)

7 tháng 4 2016
mk chưa hok tới đường trung trực nên ko làm được sorry !!!!
5454654
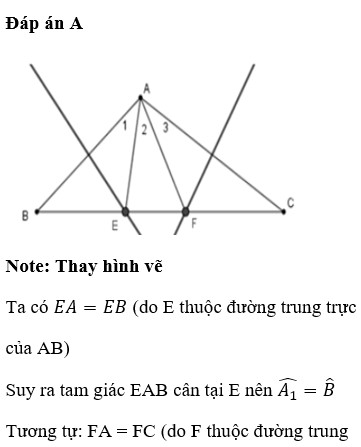
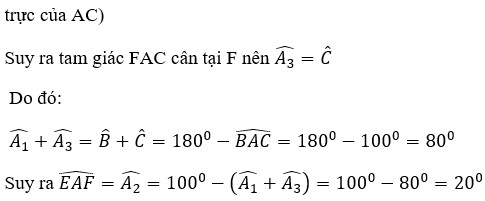
Bạn tự vẽ hình nhé!!!
a) Ta có: Các đường trung trực của AB; AC cắt nhau tại I
\(\Rightarrow\)AI là đường trung trực của BC. (3 đường trung trực cùng đi qua 1 điêm
\(\Rightarrow\)BI = CI (I nằm trên đường trung trực BC)
\(\Rightarrow\)\(\Delta IBC\) cân.
b) Xét \(\Delta\)ABC, có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\)\(\widehat{B}\) + \(\widehat{C}\) =110o
Ta có: E nằm trên đường trung trực của AB
\(\Rightarrow\) BE=AE
\(\Rightarrow\) Tam giác ABE cân
\(\Rightarrow\) \(\widehat{EBA}=\widehat{EAB}\) (1)
Ta lại có: F nằm trên đường trung trực AC
\(\Rightarrow\)AF=CF
\(\Rightarrow\) Tam giác AFC cân
\(\Rightarrow\)\(\widehat{FAC}=\widehat{FCA}\) (2)
Từ (1) và (2), ta có:
\(\widehat{EBA}+\widehat{FCA}=\widehat{EAB}+\widehat{FAC}=70^o\)
Ta có:
\(\widehat{EAF}=\widehat{BAC}-\left(\widehat{EAB}+\widehat{FAC}\right)\)
\(\widehat{EAF}=110^o-70^o\)
\(\widehat{EAF}=40^o\)
kệ m, nhờ việc ko làm thị dzẹp nhé em.