Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E
Kẻ tia Cx sao cho \(\widehat{ABD}=\widehat{ACx}\). Tia Cx cắt BD tại E
+ ΔABD ∼ ΔECD ( g.g )
\(\Rightarrow\left\{{}\begin{matrix}\frac{AD}{BD}=\frac{ED}{CD}\\\widehat{BAD}=\widehat{CEB}\end{matrix}\right.\)
=> \(AD\cdot CD=BD\cdot ED\) (1)
+ ΔABD ∼ ΔEBC ( g.g )
\(\Rightarrow\frac{AB}{BD}=\frac{EB}{BC}\Rightarrow AB\cdot BC=BD\cdot EB\) (2)
+ Từ (1) và (2) suy ra : \(AB\cdot BC-AD\cdot CD=BD\cdot EB-BD\cdot ED=BD^2\)

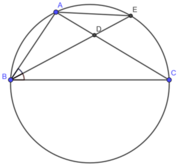
Gọi E là giao điểm của tia BD với đường tròn ngoại tiếp tam giác ABC.


O A B C D E
a, vì \(AD\) là tia phân giác của góc \(\widehat{BAC}\) \(\Rightarrow\widehat{BAD}=\widehat{EAC}\)
mà \(\widehat{ABD}=\widehat{ABC}=\widehat{AEC}\)
\(\Rightarrow\Delta ABD~\Delta AEC\) (g-g)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AC}\Leftrightarrow AB.AC=AE.AD\)
b, Ta có :
\(\widehat{EBD}=\widehat{EBC}=\widehat{EAC}=\widehat{BAE}\)
\(\Rightarrow\Delta EBD~\Delta EAB\)(g-g)
\(\Rightarrow\frac{EB}{EA}=\frac{ED}{EB}\Leftrightarrow ED.EA=EB^2\)
a)xét ΔABE và ΔADC có :
BÅE = DÅC (gt)
AEB=ACB=ACD(cùng chắn cung AB)
=>ΔABE≈ΔADC(g.g)
⇒\(\dfrac{AE}{AC}=\dfrac{AB}{AD}\)(hai cạnh t.ứ)
⇒AE.AD=AC.AB
b)Xét ΔBED và ΔAEB có :
góc E chung
góc EBD=gócEAC=gócEAB
⇒ΔBED ≈ ΔAEB(g.g)
⇒\(\dfrac{ED}{EB}=\dfrac{EB}{EA}\)(hai cạnh t.ứ)
⇒ED.EA=EB2

a) Có AH2=HF.HD \(\rightarrow\)\(\frac{AH}{HF}=\frac{HD}{AH}\)
Xét \(\Delta\)AHD và \(\Delta\)FHA có:
\(\widehat{AHD}=\widehat{FHA}=90^o\)
\(\frac{AH}{HF}=\frac{HD}{AH}\)( chứng minh trên)
\(\rightarrow\Delta\)AHD\(\approx\)\(\Delta\)FHA (c-g-c)
\(\rightarrow\)\(\widehat{ADH}=\widehat{FAH}\)( 2 góc tương ứng)
mà \(\widehat{ADH}+\widehat{HAD}=90^o\)
nên \(\widehat{FAH}+\widehat{HAD}=90^o\)
hay \(\widehat{FAD}=90^o\)\(\rightarrow\Delta\)ADF vuông tại A
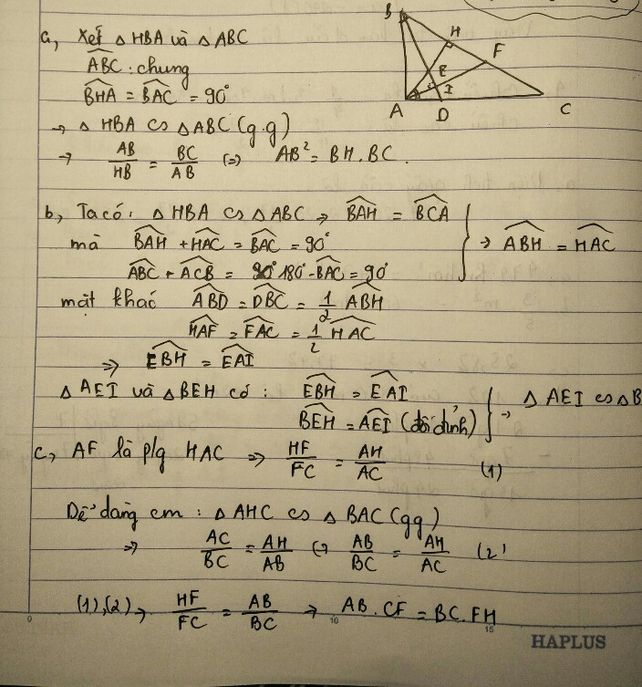
A B C D E
Kẻ tia Cx sao cho \(\widehat{ABD}=\widehat{ACx}\) . Tia Cx cắt BD tại E
+ \(\Delta ABD~\Delta ECD\left(g.g\right)\)
\(\Rightarrow\hept{\begin{cases}\frac{AD}{BD}=\frac{ED}{CD}\\\widehat{BAD}=\widehat{CEB}\end{cases}}\)
\(\Rightarrow AD.CD=BD.ED\left(1\right)\)
+ \(\Delta ABD~\Delta EBC\left(g.g\right)\)
\(\Rightarrow\frac{AB}{BD}=\frac{EB}{BC}\Rightarrow AB.BC=EB.BD\left(2\right)\)
Từ (1) và (2) suy ra
\(AB.BC-AD.DC=BD.EB-BD.ED=BD^2\)