Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N 1 2
Xét \(\Delta ABC\) ta có :
AD là tia phân giác của \(\widehat{BAC}\)
\(\Leftrightarrow\frac{AB}{AC}=\frac{BD}{DC}\) ( tính chất đường phân giác trong tam giác )
\(\Leftrightarrow\frac{AB}{AC}=\frac{MB}{NC}\)
\(\Leftrightarrow\frac{AB}{MB}=\frac{AC}{NC}\)
Xét \(\Delta ABC\) có : \(\frac{AB}{MB}=\frac{AC}{NC}\)
\(\Leftrightarrow MN//BC\) ( điịnh lí Ta - lét đảo )
Chúc bạn học tốt !!!

-Bài khó.
-Bài này mình xem cách giải của bài khá tương đồng với bài này (do GV mình giải).
-OI cắt AC tại E, AD cắt CM tại F, qua M kẻ đường thẳng song song với AC cắt BN tại G.
\(\dfrac{AN}{NC}=\dfrac{AN}{MG}.\dfrac{MG}{NC}=\dfrac{AB}{BM}.\dfrac{OM}{OC}\)
\(\Rightarrow\dfrac{OM}{OC}=\dfrac{BM}{AB}.\dfrac{AN}{NC}=\dfrac{NC}{AB}.\dfrac{AN}{NC}=\dfrac{AN}{AB}\)
\(\Rightarrow\dfrac{CM}{OC}=\dfrac{AN+AB}{AB}\Rightarrow\dfrac{OC}{CM}=\dfrac{AB}{AN+AB}\)
\(\dfrac{MF}{CF}=\dfrac{AM}{AC}\Rightarrow\dfrac{CM}{CF}=\dfrac{AM+AC}{AC}=\dfrac{AB-BM+AN+NC}{AC}=\dfrac{AB+AN}{AC}\)
\(\Rightarrow\dfrac{OC}{CM}.\dfrac{CM}{CF}=\dfrac{AB}{AN+AB}.\dfrac{AN+AB}{AC}=\dfrac{AB}{AC}\)
\(\Rightarrow\dfrac{OC}{CF}=\dfrac{AB}{AC}\Rightarrow\dfrac{CE}{AC}=\dfrac{AB}{AC}\Rightarrow CE=AB\)
\(\dfrac{IC}{DC}=\dfrac{CE}{AC}=\dfrac{AB}{AC}=\dfrac{AD}{DC}\Rightarrow IC=AD\)
\(\Rightarrow IC+ID=BD+ID\Rightarrow CD=BI\)

Giải thích các bước giải:
Do G là trọng tâm ΔABC
\(\to \frac{{GC}}{{CE}} = \frac{2}{3};\frac{{BG}}{{BD}} = \frac{2}{3}\)
Mà GM//AB; GN//AC hay GM//BE; GN//DC
Theo định lí ta-lét trong ΔCBE và BDC
\(\begin{array}{l} \to \frac{{GC}}{{CE}} = \frac{{CM}}{{CB}} = \frac{2}{3};\frac{{BG}}{{BD}} = \frac{{BN}}{{BC}} = \frac{2}{3}\\ \to \frac{{CM}}{{BC}} = \frac{{BN}}{{BC}} = \frac{2}{3} \to \frac{{BM}}{{BC}} = \frac{{CN}}{{BC}} = \frac{1}{3}\\ \to CM = BN;BM = CN\\ \to BM = MN = CN \end{array}\)

bạn tự kẻ hình nha
tam giác abc có:ad là đường phân giác (gt)
=> ab/ac=db/dc(tc đường phân giác của tam giác)
mà mb=db, nc=dc nên ta có
ab/ac=mb/nc => ab/mb=ac/nc
=> mn//bc
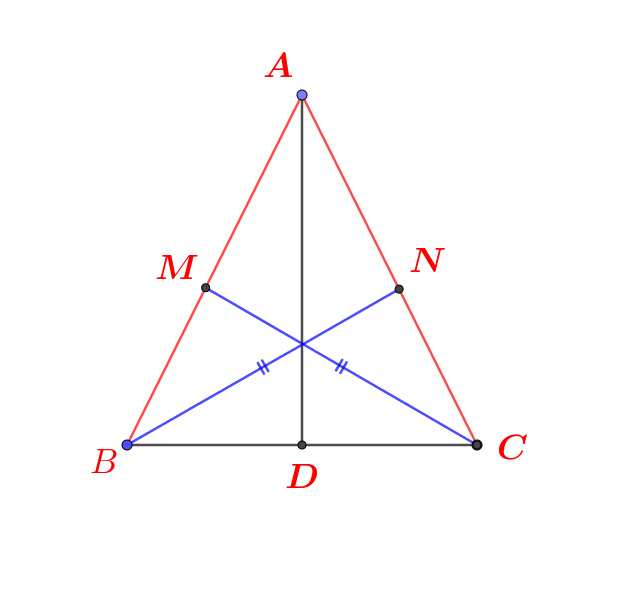
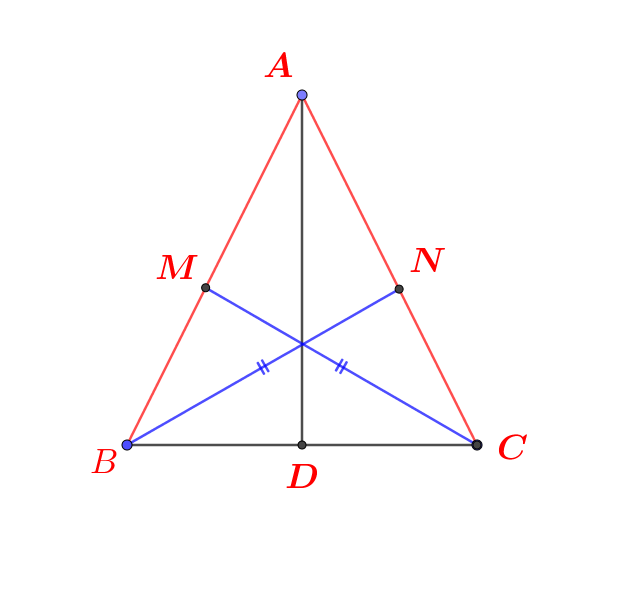
A B C D M N 1 2
Xét \(\Delta ABC\) có :
AD là tia phân giác của \(\widehat{BAC}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}\) (tính chất đường phân giác trong tam giác)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{MB}{NC}\)
\(\Leftrightarrow\dfrac{AB}{MB}=\dfrac{AC}{NC}\)
Xét \(\Delta ABC\) có : \(\dfrac{AB}{MB}=\dfrac{AC}{NC}\)
\(\Leftrightarrow MN\backslash\backslash BC\) (Định lý Ta - lét đảo)