Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, HS tự chứng minh
b, HS tự chứng minh
c, Chứng minh được: B A M ^ = M B C ^
Từ đó chứng minh được:
∆MAB:∆MBD => M B 2 = M A . M D

a: sđ cung nhỏ AB=2*30=60 độ
sđ cung lớn AB là 360-60=300 độ
góc PAB=góc BCA=30 độ
góc AOB=sđ cung nhỏ AB=60 độ
b,c: Bạn ghi lại đề đi bạn

a: Xét ΔPAC và ΔPBA có
\(\widehat{P}\) chung
\(\widehat{PAC}=\widehat{PBA}\)
Do đó:ΔPAC\(\sim\)ΔPBA
Suy ra: \(\dfrac{PA}{PB}=\dfrac{PC}{PA}\)
hay \(PA^2=PB\cdot PC\)

d, từ C kẻ đường thẳng // với PM cắt AE,AB tại Q và K
lấy H là trung điểm của BC
=>OH vuông góc với BC
H và E cùng nhìn OP dưới 1 góc 90 =>tứ giác OHEP nội tiếp =>góc MPH = góc OEH mà góc MPH = góc KCH (PM//CK) =>góc KCH= góc OEH =>tứ giác HQCE nội tiếp =>góc QHC = góc AEC mà góc AEC = góc ABC =>góc QHC=góc ABC =>QH//AB mà H là trung điểm BC
=>Q là trung điểm CK
Áp dụng định lí TA-let ta được tam giác AMO đồng dạng tam giác AKQ =>MO/KQ=AO/AQ
cmtt NO/CQ=AO/AQ mà CQ=KQ =>OM=ON

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)
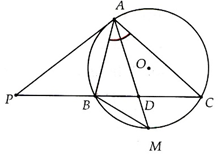
a: Sửa đề: ΔPAC\(\sim\)ΔPBA
Xét ΔPAC và ΔPBA có
\(\widehat{P}\) chung
\(\widehat{PCA}=\widehat{PAB}\)
Do đó: ΔPAC\(\sim\)ΔPBA
b: Ta có: ΔPAC\(\sim\)ΔPBA
nên PA/PB=PC/PA
hay \(PA^2=PB\cdot PC\)