Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: góc HBC+góc HCB=90 độ-góc ABC+90 độ-góc ACB
=góc BAC
=>góc BHC=180 độ-góc BAC
=>góc BHC+góc BAC=180 độ
H đối xứng M qua BC
=>BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
=>ΔBHC=ΔBMC
=>góc BMC=góc BHC
=>góc BMC+góc BAC=180 độ
=>ABMC nội tiếp
c: Xét tứ giác BHCN có
BC cắt HN tại trung điểm của mỗi đường
=>BHCN là hìnhbình hành
=>góc BHC=góc BNC
=>góc BNC+góc bAC=180 độ
=>ABNC nội tiếp

A B C M
Tớ thử làm trường hợp tam giác ABC đều,còn tam giác thường chắc nhờ cô Linh Chi cứu
Tứ giác ABMC nội tiếp ( O ) nên theo định lý Ptoleme ta có \(BM\cdot AC+MC\cdot AB=BC\cdot AM\)
\(\Leftrightarrow BM+CM=AM\)
Theo BĐT Ba Con Sâu ta có:\(\frac{1}{MB}+\frac{1}{MC}\ge\frac{4}{MA}\ge\frac{4}{2R}=2R\)
Dấu "=" xảy ra tại M là điểm chính giữa cung BC

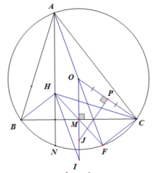
Ta có NHC = ABC (cùng phụ với HCB) (1)
Vì ABDC là tứ giác nội tiếp nên ABC = ADC (2)
Vì D và E đối xứng nhau qua AC nên AC là trung trực DE suy ra
∆ADC = ∆AEC (c.c.c) => ADC = AEC (3)
Tương tự ta có AEK = ADK
Từ (1), (2), (3) suy ra NHC = AEC => AEC + AHC = NHC + AHC = 180o
Suy ra AHCE là tứ giác nội tiếp => ACH = AEK = ADK (đpcm)