Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

Gọi I là giao điểm của phân giác góc B và C
Xét tam giác HAC vuông tại H và tam giác ABC vuông tại A có góc C chung => góc HAC = góc ABC
Ta có: góc ADC = góc DAB + góc DBA = góc DAH + góc HAC ( vì góc DAB = DAH ; góc HAC=DBA)
=>góc ADC= góc DAH + góc HAC = góc DAC
=> tam giác CAD cân tại C => CA=CD
tam giác CID = tam giác CIA (c.g.c) => IA = ID (1)
CM tương tự, ta có IA = IE (2)
Từ (1) và (2) suy ra IA = IE = ID => I là giao điểm 3 đường trung trực của tam giác ADE
=> đpcm

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

A B C I 1 2 3 4 5 6
\(I_1+I_2=360^0-90^0-90^0-A=140^0\)
\(I_2=I_3;I_1=I_6\)
\(\Rightarrow I_1+I_2+I_3+I_6=2.140=280^0\)
\(\Rightarrow BIC = 360^0-280^0=80^0\)
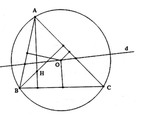
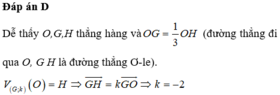
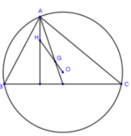


Đáp án D
Các quy tắc A, B, C đều biến O thành nhiều hơn một điểm nên đó không phải là phép biến hình. Quy tắc D biến O thành điểm H duy nhất nên đó là phép biến hình.