Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C B H D M O K
a/ Ta có
\(\widehat{ACK}=90^o\) (góc nội tiếp chắn nửa đường tròn)\(\Rightarrow CK\perp AC\)
\(BH\perp AC\) (BH là đường cao)
=> BH//CK (vì cùng vuông góc với AC) (1)
Ta có
\(\widehat{ABK}=90^o\) (góc nội tiếp chắn nửa đường tròn)\(\Rightarrow BK\perp AB\)
\(CH\perp AB\) (CH là đường cao)
=> CH//BK (cùng vuông góc với AB (2)
Từ (1) và (2) => BHCK là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một thì tứ giác đó là hbh)
b/ Nối BO cắt đường tròn tại D ta có
\(\widehat{BCD}=90^o\) (góc nội tiếp chắn nửa đường tròn)\(\Rightarrow CD\perp BC\)
\(AH\perp BC\) (AH là đường cao)
=> AH//CD (cùng vuông góc với BC) (3)
Ta có
\(\widehat{BAD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AD\perp AB\)
\(CH\perp AB\) (CH là đường cao)
=> AD//CH (cùng vuông góc với AB) (4)
Từ (3) và (4) => AHCD là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một thì tứ giác đó là hbh)
=> AH=CD (trong hbh các cặp cạnh đối bằng nhau từng đôi một)
Xét \(\Delta BCD\) có
\(BM=CM;BO=DO\) => OM là đường trung bình của \(\Delta BCD\Rightarrow OM=\frac{1}{2}CD\)
Mà \(CD=AH\Rightarrow OM=\frac{1}{2}AH\left(dpcm\right)\)

tam 0 chinh la giao diem 3 dg trung truc, OMHA la hbh => AH=OM
vay AH/OM = 1
MK GIU DUNG LOI HUA NHE chuc bạn hoc gioi

Tổng quát cho câu 2 là định lí Ptolemy, như sau: Cho \(ABCD\) nội tiếp bất kì. Khi đó \(AC.BD=AB.CD+AD.BC\).
A B C D E
CM: Vẽ \(E\in AC\) sao cho \(\widehat{ABD}=\widehat{EBC}\).
Khi đó có hai tam giác sau đồng dạng \(ABD\) và \(EBC\), \(ABE\) và \(DBC\).
Suy ra tỉ lệ cạnh: \(\frac{AD}{EC}=\frac{BD}{BC}\) và \(\frac{AB}{DB}=\frac{AE}{DC}\).
Hay \(AD.BC=BD.EC\) và \(AB.DC=AE.DB\)
Cộng lại: \(AB.CD+AD.BC=BD\left(AE+EC\right)=AC.BD\)

AH vuông góc BC và KB vuông góc CB nên AH//BK
Lại có BH vuông góc AC và KA vuông góc CA nên HB//AK
Xét tứ giác AHBK có: AH//BK và HB//AK nên AHBK là hình bình hành
Suy ra AH=BK
Xét (O;R) có:
CK là đường kính của (O;R)
Điểm C; B; K thuộc (O;R)
Suy ra: tam giác CBK vuông tại B
Áp dụng dịnh lý py-ta-go cho tam giác CBK vuông tại B
Có: BK^2+CB^2=CK^2
Mà AH=BK(cmt)
Suy ra: AH^2+ BC^2=CK^2 (1)
Có CK là đường kính
Suy ra CK=2R tương đương CK^2=4R^2 (2)
Adđl py-ta-go cho các tam giac AA'B; CHA'; BAB'; BB'C
Có: AB^2=AA'^2+BA'^2
CH^2=CA'^2+HA'^2
AH^2=AB'^2+HB'^2
BC^2=BB'^2+B'C^2
Suy ra: AB^2+CH^2=( AA'^2+CA'^2 ) + ( BA'^2+HA'^2 )= AC^2+BH^2 (3)
=) AH^2+BC^2= BB'^2+AB'^2+HB'^2+B'C^2=AB^2+CH^2 (4)
Từ (1) ; (2) ;(3) và (4) =) AH^2+BC^2= BH^2+AC^2=CH^2+AB^2=4R^2 (đpcm)


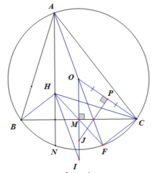
a) Gọi F là điểm đối xứng với A qua O ⇒ AF là đường kính của (O)
Ta có ACF = ABF = 90o (góc nội tiếp chắn nửa đường tròn) ⇒ AC ⊥ CF , AB ⊥ BF
Mà BH ⊥ AC, CH ⊥ AB ⇒ CF // BH, BF // HC
Suy ra BHCF là hình bình hành ⇒ Trung điểm M của BC cũng là trung điểm của HF.
⇒ OM là đường trung bình của ∆ AHF ⇒ AH = 2OM