Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

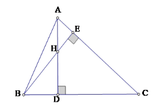
Xét tam giác vuông ABD và ADC, ta có tan B = A D B D ; tan C = A D C D
Suy ra: tan B . tan C = A D 2 B D . C D (1)
Lại có: H B D ^ = C A D ^ (cùng phụ với A C B ^ ) và H D B ^ = A D C ^ = 90 0
Do đó ∆ B D H ~ ∆ A D C (g.g), suy ra D H D C = B D A D , do đó BD.DC = DH.AD (2)
Từ (1) và (2) suy ra tan B . tan C = A D 2 D H . A D = A D D H (3)
Theo giả thiết H D A H = 1 2 suy ra H D A H + H D = 1 2 + 1 hay H D A D = 1 3 , suy ra AD = 3HD
Thay vào (3) ta được: tan B . tan C = 3 H D D H = 3
Đáp án cần chọn là: B

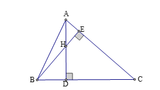
Xét tam giác vuông ABD và ADC, ta có: tan B = A D B D ; tan C = A D C D
Suy ra: tan B . tan C = A D 2 B D . C D (1)
Lại có H B D ^ = C A D ^ (cùng phụ với A C B ^ ) và H D B ^ = A D C ^ = 90 0
Do đó ∆ B D H ~ ∆ A D C (g.g), suy ra D H D C = B D A D , do đó BD.DC = DH.AD (2)
Từ (1) và (2) suy ra tan B . tan C = A D 2 D H . A D = A D D H (3)
Theo giả thiết H D A H = 3 2 suy ra H D A H + H D = 3 2 + 3 hay H D A D = 3 5 , suy ra AD = 5 3 HD
Thay vào (3) ta được: tan B . tan C = 5 3 H D D H = 5 3
Đáp án cần chọn là: D

b: góc HID+góc HKD=180 độ
=>HIDK nội tiếp
=>góc HIK=góc HDK
=>góc HIK=góc HCB
=>góc HIK=góc HEF
=>EF//IK

Đề thì đúng nhưng đề này là đề học sinh giỏi thì thường quá!
Bạn chỉ cần dùng tứ giác nội tiếp là sẽ ra \(DH\) là phân giác \(\widehat{EDF}\) (tin mình đi). Tương tự với mấy đỉnh kia suy ra đpcm.
sai đề rồi đáng lẽ ABC là tam giác đều hoặc các đường cao AD BE CF là những đường trung trực

A B C D E F H
Xét ∆ABE và ∆ACF có:
\(\widehat{A}\left(chung\right)\)
\(\widehat{AEB}=\widehat{AFC}\left(=90^0\right)\)
\(\Rightarrow\)∆ABE ~ ∆ACF (g-g)
\(\Rightarrow\frac{AE}{AF}=\frac{AB}{AC}\Rightarrow\frac{AE}{AB}=\frac{AF}{AC}\)
Xét ∆AEF và ∆ABC có:
\(\frac{AE}{AB}=\frac{AF}{AC}\left(cmt\right)\)
\(\widehat{A}\left(chung\right)\)\
\(\Rightarrow\)∆AEF ~ ∆ABC (đpcm)
Ta có: \(\tan B=\frac{ÁD}{DB};\tan C=\frac{AD}{DC}\)
Xét ∆ADC và ∆BDH có:
\(\widehat{HBD}=\widehat{CAD}\)( cùng phụ với \(\widehat{C}\))
\(\widehat{ADC}=\widehat{BDH}\left(=90^0\right)\)
\(\Rightarrow\)∆ADC ~ ∆ BDH (g-g)
\(\Rightarrow\frac{AD}{DC}=\frac{BD}{DH}\)
\(\Rightarrow\tan B\cdot\tan C=\frac{AD}{DB}\cdot\frac{AD}{DC}=\frac{AD}{DB}\cdot\frac{BD}{DH}=\frac{AD}{DH}\)(đpcm)

Bài 1:
A B C H F D E K L
+) Chứng minh tứ giác BFLK nội tiếp:
Ta thấy FAH và LAH là hai tam giác vuông có chung cạnh huyền AH nên AFHL là tứ giác nội tiếp. Vậy thì \(\widehat{ALF}=\widehat{AHF}\) (Hai góc nội tiếp cùng chắn cung AF)
Lại có \(\widehat{AHF}=\widehat{FBK}\) (Cùng phụ với góc \(\widehat{FAH}\) )
Vậy nên \(\widehat{ALF}=\widehat{FBK}\), suy ra tứ giác BFLK nội tiếp (Góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện)
+) Chứng minh tứ giác CELK nội tiếp:
Hoàn toàn tương tự : Tứ giác AELH nội tiếp nên \(\widehat{ALE}=\widehat{AHE}\) , mà \(\widehat{AHE}=\widehat{ACD}\Rightarrow\widehat{ALE}=\widehat{ACD}\)
Suy ra tứ giác CELK nội tiếp.
GIÚP MÌNH VỚI NHAAAA <33333