Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Do các tứ giác BFEC ,DEIC , ABDE nội tiếp nên: \(\widehat{AFE}=\widehat{ACB}=\widehat{DIE}\)
\(\widehat{MEC}=\widehat{ABC}=\widehat{DEC}=\widehat{DIC}\Rightarrow\)Tứ giác MENI nội tiếp
\(\Rightarrow\widehat{DIE}=\widehat{EMN}\Rightarrow\widehat{AFE}=\widehat{EMN}\Rightarrow MN//AB\)
Mà \(CH\perp AB\Rightarrow CH\perp MN\left(đpcm\right)\)
b) Xét \(\Delta ENM\)và \(\Delta TNC\)có: \(\widehat{EMN}=\widehat{EIN}=\widehat{NCT},\widehat{ENM}=\widehat{TNC}\Rightarrow\Delta ENM~\Delta TNC\left(g.g\right)\)
\(\Rightarrow\frac{NE}{NT}=\frac{NM}{NC}\Rightarrow NC.NE=NM.NT\left(1\right)\)
Xét \(\Delta ENK\)và \(\Delta GNC\)có: \(\widehat{KEN}=\widehat{CGN},\widehat{ENK}=\widehat{GNC}\Rightarrow\Delta ENK~\Delta GNC\left(g.g\right)\)
\(\Rightarrow\frac{NE}{NG}=\frac{NK}{NC}\Rightarrow NE.NC=NG.NK\left(2\right)\)
Từ (1) và (2) suy ra \(NM.NT=NG.NK\Rightarrow\frac{NK}{NT}=\frac{NM}{NG}\Rightarrow\Delta TGN~\Delta KMN\)
\(\Rightarrow\widehat{KMN}=\widehat{TGN}\left(3\right)\)
Mà \(\widehat{KMN}=\widehat{HCK}\)(cùng phụ với \(\widehat{KHC}\))\(\Rightarrow\widehat{KMN}=\widehat{HGN}\)(4)
Từ (3) và (4) suy ra \(\widehat{TGN}=\widehat{HGN}\Rightarrow\)H, T, G thẳng hàng (đpcm)

Giải chi tiết:
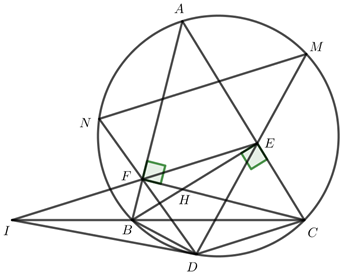
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.

a) Xét tứ giác DHEC có
\(\widehat{HDC}\) và \(\widehat{HEC}\) là hai góc đối
\(\widehat{HDC}+\widehat{HEC}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: DHEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

A B C D E F H I N M T K O F
Ta có tứ giác AEDB nội tiếp (AB), tứ giác BFEC nội tiếp (BC) nên ^CID = ^CED = ^ABD = ^AEF = ^MEN
=> Tứ giác MINE nội tiếp => ^EMN = ^EIN = ^ECT => Tứ giác EMCT nội tiếp
Áp dụng hệ thức lượng trong đường tròn: NM.NT = NE.NC = NF.NK => Tứ giác MKTF nội tiếp
=> ^FKT = ^FMT = ^HMN. Cũng từ tứ giác MINE nội tiếp ta suy ra ^EMN = ^ECT = ^AFE
=> MN // AF. Mà AF vuông góc CH nên MN vuông góc CH
Kết hợp với ^HFC chắn nửa đường tròn (O) suy ra ^HMN = ^HCF (Cùng phụ ^MHC)
Do đó ^FKT = ^HCF = ^FKH. Vì H,T nằm cùng phía so với FK nên KT trùng KH
Vậy thì H,K,T thẳng hàng (đpcm).