
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TC
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên

14 tháng 7 2021
Áp dụng hệ quả của định lý Cosin ta có:
\(\cos C=\dfrac{b^2+a^2-c^2}{2ab};\cos B=\dfrac{c^2+a^2-b^2}{2ca}\)
\(\Rightarrow b\cos C+c\cos B=b\dfrac{b^2+a^2-c^2}{2ab}+c\dfrac{c^2+a^2-b^2}{2ca}=\)
\(\dfrac{b^2+a^2-c^2}{2a}+\dfrac{c^2+a^2-b^2}{2a}=\dfrac{2a^2}{2a}=a\)



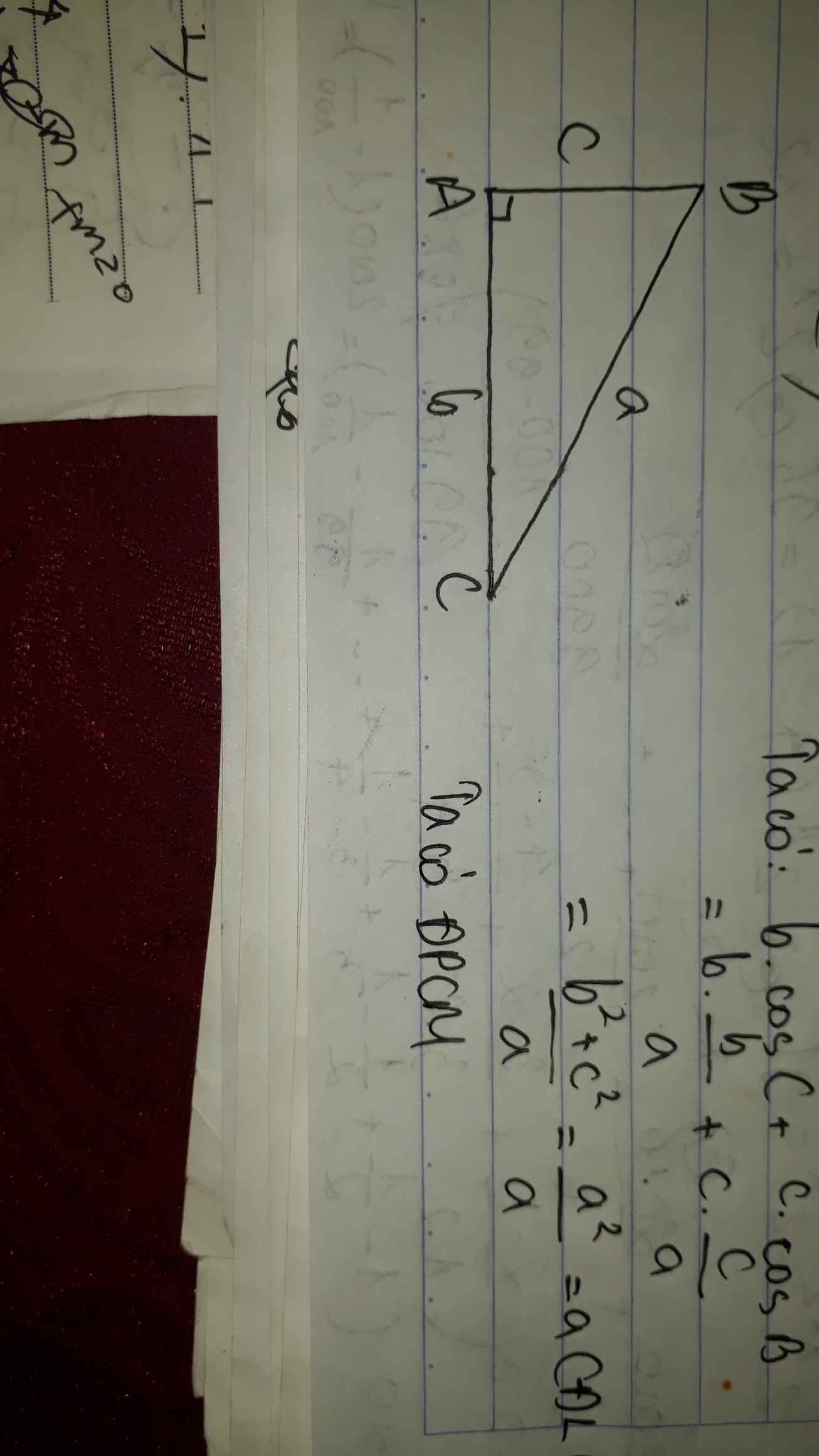
AB/sinC = BC/sinA = CA/sinB cái này là định lý hàm số sin nè: chứng minh một cạnh của tam giác bằng đường kính nhân sin góc đối là ra
cosA + cosB + cosC > (sinA + sinB + sinC)/2: kẻ 3 đg` cao AD BE CF cắt nhau tại H
=> cosB=cosAHF=HF/AH, cosC=cosAHE=HE/AH
EF=AH.sinA => sinA = EF/AH
EF<HF + HE(bđt tam giác)
=> sinA < cosB + cosC
chứng minh tương tự => đpcm