Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu C bạn cm AFCE là hình chữ nhật , FE là đường chéo => E,F,M thẳng hàng vì 2 đường chéo hình chữ nhật đi qua trung điểm của mỗi đường.

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét ΔMBA và ΔMCD có
MB=MC
\(\widehat{AMB}=\widehat{DMC}\)
MA=MD
Do đó: ΔMBA=ΔMCD

a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
DO đó; ΔABM=ΔCDM
b: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó:ABCD là hình bình hành
Suy ra: AB//CD

Ta có hình vẽ:
a/ Xét tam giác AMD và tam giác CMB có
AM = MC (GT)
\(\widehat{AMD}\)=\(\widehat{CMB}\) (đối đỉnh)
MD = MB (GT)
Vậy tam giác AMD = tam giác CMB (c.g.c)
b/ Ta có: tam giác AMB = tam giác CMB (câu a)
=> \(\widehat{BCM}\)= \(\widehat{MAD}\)
Mà góc BCM; MAD ở vị trí so le trong
=> AD // BC (đpcm)
c/ Xét tam giác ABC và tam giác CDA có:
AC: cạnh chung
AD = BC (vì tam giác AMD = tam giác CMB)
\(\widehat{BCM}\)=\(\widehat{MAD}\)
Vậy tam giác ABC = tam giác CDA (c.g.c)
d/ Ta có: tam giác ABC = tam giác CDA (câu c)
=> \(\widehat{BAC}\) =\(\widehat{ACD}\)
Mà góc BAC; ACD ở vị trí so le trong
=> AB // CD (đpcm)
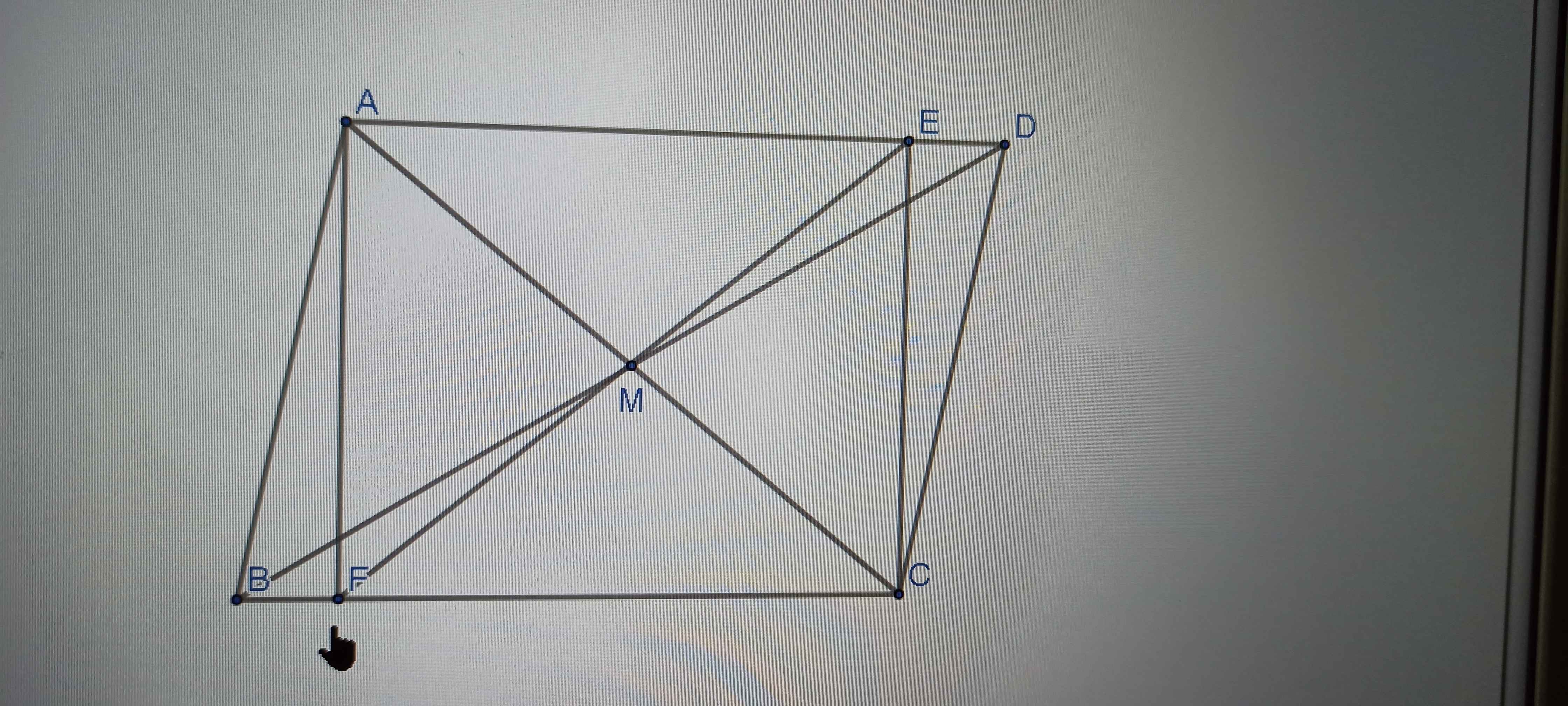

a: Xét ΔMAB và ΔMCD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đo: ΔMAB=ΔMCD
b: \(\Leftrightarrow2\cdot BM< AB+BC\)
\(\Leftrightarrow CD+BC>BD\)(luôn đúng)