Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ôi xin lỗi nhé,nhưng mình không hiểu cái đề bài cho lắm!

a) Xét \Delta AMBΔAMB và \Delta DMCΔDMC có:
AB=AC(gt)
AM=MD(gt)
MB=MC(gt)
=>\Delta AMB=\Delta DMC\left(c.c.c\right)ΔAMB=ΔDMC(c.c.c)
b) Vì: \Delta AMB=\Delta DMC\left(cmt\right)ΔAMB=ΔDMC(cmt)
=> \widehat{MAB}=\widehat{MDC}MAB=MDC . Mà hai góc này ở vị trí sole trong
=>AB//DC
# Study well 'v'
a) Xét \(\Delta AMB\) và \(\Delta DMC\) , ta có:
AB = AC (gt)
AM=MD (gt)
MD=MC (gt)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.c.c\right)\)
b) Vì: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB=\widehat{MDC}}\)
\(\Rightarrow AB\) // \(DC\)
#Chúc bạn học tốt ^^

1 Xét 2 tam giác MAB và tam giác MDC:
Ta thấy:
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
BM=MC (gt)
MA=MD (gt)
Từ các giả thiết trên, suy ra:
\(\Delta MAB=\Delta MDC\left(c-g-c\right)\)

a/ Xét tam giác AMB và tam giác DMC có:
MA= MD( GT)
AMB=CMD( 2 góc đối đỉnh)
MB= MC( M là trung điểm của BC)
=> tam giác AMB= tam giác DMC(c.g.c)
b/ => góc BAM=MDC( theo a)
=> AB// CD( 2 góc ở vị trí sole trong bằng nhau)
c/ Xét tam giác AEM và tam giác AFM có:
AE= EF(GT)
góc EAM= FDM( theo b)
AM= DM( GT)
=> tam giác AEM = tam giác AFM(c.g.c)
Do đó: góc AME= góc DMF
=>góc AME+ AMF= DMF+ AMF
=>EMF= 180 độ
Vậy => E, M, F thẳng hàng.
Xin lỗi ! Bạn có thể tự vẽ hình dc ko?

a) CM : tam giác ABM = tam giác DCM
Xét tam giác ABM và tam giác DCM có:
BM = CM ( M là trung điểm của BC )
MA = MD ( gt )
góc BMA = góc CMD ( đối đỉnh )
=> tam giác ABM = tam giác DCM ( c- g - c)
b ) CM AB // CD
Theo chứng minh trên, ta có:
góc BAM = góc CDM ( 2 góc tương ứng của tam giác ABM = tam giác DCM )
mà hai góc này ở vị trí so le trong nên AB // CD
-------
Bạn nên vẽ hình và dùng kí hiệu ra nha, mình ghi nhanh giải cho bạn thôi <3

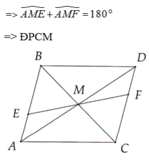
a: Sửa đề: ΔAMB=ΔDMC
Xét ΔAMB và ΔDMC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔAMB=ΔDMC
b: Xét ΔABC và ΔDCB có
AB=DC
góc ABC=góc DCB
BC chung
=>ΔABC=ΔDCB