Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Youcho tam giác nhọn ABC, AB<AC. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD a) chứng minh tam giác AMB=tam giác DMC b) chứng minh AB=DC c)chứng minh AB song song với CD
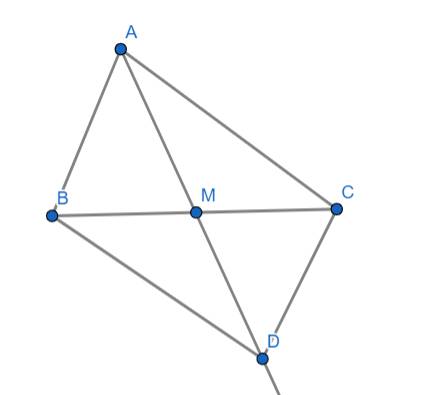
a) Xét ΔAMB và ΔDMC có:
\(AM=CM\) (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(BM=CM\) (M là trung điểm của BC)
\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)
b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow AB=DC\) (2 cạnh t.ứng)
c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
bạn tự vẽ hình nha
vì \(\widehat{AMB}\) và \(\widehat{CMD}\) là 2 góc đối đỉnh
⇒\(\widehat{AMB}\) = \(\widehat{CMD}\)
Xét Δ AMB và Δ CMD, có:
\(\widehat{AMB}\) = \(\widehat{CMD}\) (cmt)
AM=MD (gt)
MA=MB( vì M là trung điểm BC)
⇒Δ AMB = Δ CMD (c.g.c)
⇒\(\widehat{MAB}=\widehat{MDC}\) (2 góc tương ứng)
Mà đây là 2 góc so le trong
⇔AB // CD( đpcm)
Bạn tự vẽ hình nha, mình lười lắm
❉Ta có: góc AMB = góc CMD ( 2 góc đối đỉnh )
❉Xét Δ AMB Δ CMD, ta có:
- AM = MD (gt)
- Góc AMB = CMD (cmt)
- MA = MB ( vì M là trung điểm của BC)
➤ Δ AMB = Δ CMD (c.g.c)
➤ Góc MAB = góc MDC (2 góc tương ứng)
mà đây lại là 2 góc sole trong ➢ AB // CD (đpcm)
a, Xét tam giác AMB và tam giác DMC có
AM = DM ; BM = MC ; ^AMB = ^DMC (đ.đ)
Vậy tam giác AMB = tam giác DMC (c.g.c)
=> ^ABM = ^DCM ( 2 góc tương ứng )
mà 2 góc này ở vị trí đồng vị
Vậy AB // CD
Ôi xin lỗi nhé,nhưng mình không hiểu cái đề bài cho lắm!
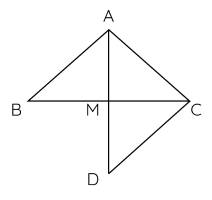
a) Xét hai tam giác $AMB$ và $AMC$ có:
$AM$ là cạnh chung;
$AB = AC$ (gt);
$BM = MC$ ($M$ là trung điểm $BC$);
Suy ra $\Delta AMB=\Delta AMC$ (c.c.c)
b) $\Delta AMB=\Delta AMC$ suy ra
$\widehat{BAM} = \widehat{CAM}$ (hai góc tương ứng)
Suy ra $AM$ là tia phân giác của góc $BAC$.
c) Xét hai tam giác $AMD$ và $DMC$ có:
$AM = AD$ (gt);
$\widehat{AMB} = \widehat{CMD}$ (hai góc đối đỉnh);
$BM = MC$.
Nên $\Delta AMD=\Delta DMC$ (c.g.c)
Suy ra $\widehat{BAM} = \widehat{CDM}$ (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong nên $AB$ // $CD$.
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB=DC
a) Sửa đề: ΔAMB=ΔDMC
Xét ΔAMB và ΔDMC có
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔDMC(c-g-c)