Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$ nên:
$BD=20:(3+4).3=\frac{60}{7}$ (cm)
$CD= 20:(3+4).4=\frac{80}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD = BD-BH = \frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD = \sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)

a) Xét \(\Delta HAC\) và \(\Delta ABC\) có :
Góc AHC = góc BAC = 90o; góc C chung
=> \(\Delta HAC\) đồng dạng với \(\Delta ABC\) (g.g)
b) Vì \(\Delta ABC\) vuông tại A nên AB2 + AC2 = BC2 => AB2 = BC2 - AC2 = 202 - 162 = 144
=> \(AB=\sqrt{144}=12\left(cm\right)\)
Từ a) => \(\frac{AH}{AB}=\frac{AC}{BC}\) hay \(\frac{AH}{6}=\frac{8}{10}\) => \(AH=\frac{6.8}{10}=4,8\left(cm\right)\)
c) Ta có \(\Delta ABD\) đồng dạng với \(\Delta HBI\) (g.g) ('Bạn tự chứng minh')
=> Góc BIH = góc ADB
Mà góc BIH = góc AID (đ2) => Góc AID = góc ADB
=> Tam giác AID cân tại A
d) ('Mình ko biết')
a) Xét \(\Delta HAC\) và \(\Delta ABC\) có :
Góc AHC = góc BAC = 90o; góc C chung
=> \(\Delta HAC\) đồng dạng với \(\Delta ABC\) (g.g)
b) Vì \(\Delta ABC\) vuông tại A nên AB2 + AC2 = BC2 => AB2 = BC2 - AC2 = 202 - 162 = 144
=> \(AB=\sqrt{144}=12\left(cm\right)\)
Từ a) => \(\frac{AH}{AB}=\frac{AC}{BC}\) hay \(\frac{AH}{6}=\frac{8}{10}\) => \(AH=\frac{6.8}{10}=4,8\left(cm\right)\)
c) Ta có \(\Delta ABD\) đồng dạng với \(\Delta HBI\) (g.g) ('Bạn tự chứng minh')
=> Góc BIH = góc ADB
Mà góc BIH = góc AID (đ2) => Góc AID = góc ADB
=> Tam giác AID cân tại A

Xét ΔABC có AD là đường phân giác
nên AB/AC=BD/CD
=>AB/AC=3/4
=>HB/HC=9/16
=>\(HB=17.5\cdot\dfrac{9}{25}=6.3\)
=>HC=11,2
=>AH=8,4
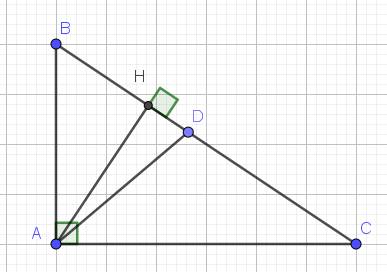
Xét ΔABC có AD là đường phân giác
nên AB/AC=BD/CD=3/4
=>BH/CH=9/16
=>BH=6,3
=>CH=11,2
=>AH=8,4