Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do N nằm giữa A và C nên: NC = AC - AN = 13,5 - 6 = 7,5cm
Ta có:
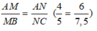
Suy ra: MN // BC ( định lí Ta let đảo)
Theo hệ quả định lí ta let ta có;
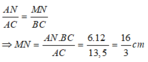
Chọn đáp án B

M nằm giữa A và B nên: AB = AM + MB = 10cm
Theo định lí Ta let ta có:
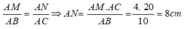
Chọn đáp án A

NC=9-4=5cm
Xét ΔABC có MN//BC
nên AM/MB=AN/NC
=>3/MB=4/5
=>MB=3:4/5=3*5/4=15/4=3,75cm
AB=3+3,75=6,75cm
\(BC=\sqrt{6.75^2+9^2}=11.25\left(cm\right)\)
MN/BC=AM/AB
=>MN/11,25=3/6,75=4/9
=>MN=5(cm)

Xét ΔANN' có MM'//NN'
nên \(\dfrac{AM}{AN}=\dfrac{MM'}{NN'}\)
=>5/NN'=1/2
=>NN'=10(cm)
Xét hình thang MM'CB có
N là trung điểm của MB
NN'//MM'//CB
Do đó: N' là trung điểm của M'C
Xét hình thang MM'CB có
N là trung điểm của MB
N' là trung điểm của M'C
Do đó: NN' là đường trung bình
=>NN'=(MM'+BC)/2
=>5+BC=20
=>BC=15(cm)

Xét ΔABC có MN//BC
nên AM/AB=AN/AC
=>AN/20=4/20=1/5
nên AN=4(cm)

BM=AB-AM=2cm
Xét ΔABC có MN//BC
nên AM/MB=AN/NC
=>3/NC=2
hay NC=1,5(cm)
=>CA=4,5(cm)
\(BC=\sqrt{6^2+4.5^2}=7.5\left(cm\right)\)







b) Ta có: AN+NB=AB(N nằm giữa A và B)
nên AB=9+10,5=19,5(cm)
Xét ΔABC có
N\(\in\)AB(gt)
M\(\in\)AC(gt)
MN//BC(gt)
Do đó: \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{9}{19.5}=\dfrac{AM}{8.5}\)
\(\Leftrightarrow AM=\dfrac{9\cdot8.5}{19.5}=\dfrac{51}{13}cm\)
Vậy: \(AM=\dfrac{51}{13}cm\)