Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
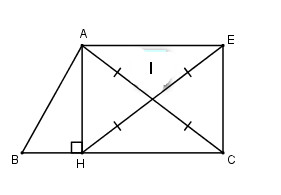
Theo giả thiết II là trung điểm của ACAC nên IA=ICIA=IC
EE là điểm đối xứng với HH qua II nên II là trung điểm của HEHE hay IE=IHIE=IH
Tứ giác AHCEAHCE có hai đường chéo cắt nhau tại trung điểm mỗi đường do đó là hình bình hành (theo dấu hiệu nhận biết 4)
Mặt khác AHAH là đường cao nên ˆAHC=900AHC^=900
Do đó AHCEAHCE là hình chữ nhật (theo dấu hiệu nhận biết 3)
giác AHCE là hình gì ? Vì sao ?
Bài giải:
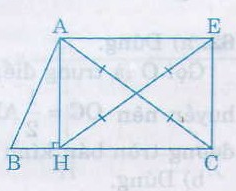
Ta có IA = IC (gt)
IE = IH (gt)
Nên AHCE là hình bình hành (dấu hiệu nhận biết 4)
Lại có ˆAHCAHC^ =1v
Nên AHCE là hình chữ nhật (dấu hiệu nhận biết 3) (Hoặc hình bình hành AHCE là hình chữ nhật vì có hai đường chéo bằng nhau).

Xét tứ giác AHCE có
I là trung điểm chung của AC và HE
=>AHCE là hình bình hành
Hình bình hành AHCE có \(\hat{AHC}=90^0\)
nên AHCE là hình chữ nhật

a: Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
b: Ta có: AHCD là hình chữ nhật
=>\(AC^2=AD^2+AH^2\)
=>\(AC^2=6^2+8^2=100\)
=>\(AC=\sqrt{100}=10\left(cm\right)\)
Ta có: ΔAHC vuông tại H
mà HI là đường trung tuyến
nên \(HI=\dfrac{AC}{2}=5\left(cm\right)\)

Hình đó là hình Chữ Nhật, CM:
Xét hình Tứ Giác AECH có \(IA=IC;IH=IE\Rightarrow\)tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hình Bình Hành. Mà góc AHC vuông
\(\Rightarrow\)AEHC là hình Chữ Nhật vì hình Bình Hành có 1 góc là hình Chữ Nhật

a: Xét tứ giác AHCE có
D là trung điểm chung của AC và HE
góc AHC=90 độ
Do đó: AHCE là hình chữ nhật
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
=>BC=2*BH=6cm
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot4=2\cdot6=12\left(cm^2\right)\)

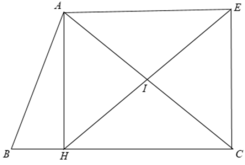
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = 1/2AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = 1/2HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có E A H ^ = A H C ^ = H C E ^ = C E A ^ = 90 0
⇒ AHCE là hình chữ nhật.

a: Xét tứ giác AHCE có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
b: Xét ΔAHB có
K là trung điểm của AB
M là trung điểm của BH
Do đó: KM là đường trung bình của ΔAHB
Suy ra: KM//AH
hay KM\(\perp\)BH
Xét ΔAHC có
I là trung điểm của AC
N là trung điểm của HC
Do đó: IN là đường trung bình của ΔAHC
Suy ra: IN//AH
hay IN\(\perp\)BC
Xét ΔABC có
K là trung điểm của AB
I là trung điểm của AC
Do đó: KI là đường trung bình của ΔBAC
Suy ra: KI//BC
hay KI\(\perp\)AH
mà AH//KM
nên KI\(\perp\)KM
Xét tứ giác KINM có
\(\widehat{IKM}=\widehat{KMN}=\widehat{INM}=90^0\)
Do đó: KINM là hình chữ nhật
Suy ra: KN=IM

I là trung điểm của AC ⇒ IA = IC.
E đối xứng với H qua I ⇒ IE = IH
⇒ AC ∩ HE = I là trung điểm của AC và HE
⇒ AHCE là hình bình hành (dấu hiệu nhận biết 4)
Lại có : Ĥ = 90º
⇒ AHCE là hình chữ nhật (đpcm).