Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
. Chu vi tam giác ABC là 12cm, thì chu vi tam giác DEF là: 
Gọi x(cm) là độ dài cạnh của hlp ( x > 0 )
Theo định lí Pythagoras ta có : \(2x^2=25\Leftrightarrow x=\frac{5\sqrt{2}}{2}\left(cm\right)\)vì x > 0
\(\Rightarrow S_{tp}=\left(\frac{5\sqrt{2}}{2}\right)^2\cdot6=75cm^2\)
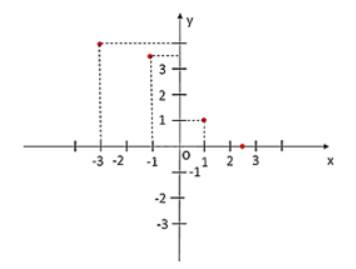
a có tập hợp các điểm của đồ thị hàm số y = f(x) là
{(– 3; 4); (– 1; 3,5); (1; 1); (2,5; 0)}.
Biểu diễn các điểm trên lên mặt phẳng tọa độ Oxy ta được đồ thị của hàm số y = f(x).
a) \(y=ax+3\)
Khi \(x=1;y=5\)
\(\Rightarrow5=a.1+3\)
\(\Rightarrow a=2\)
\(\Rightarrow y=2x+3\)
b) \(x=-2\Rightarrow y=-1\)
\(x=-1\Rightarrow y=1\)
\(x=0\Rightarrow y=3\)
\(x=1\Rightarrow y=5\)
\(x=2\Rightarrow y=7\)
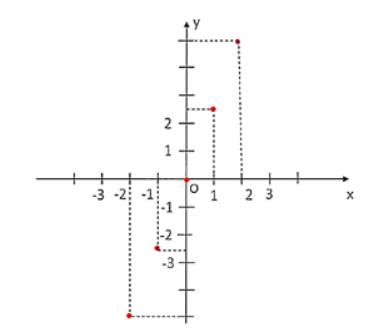
Tập hợp các điểm của đồ thị hàm số y = f(x) là
{(– 2; – 5); (– 1; – 2,5); (0; 0); (1; 2,5); (2; 5)}.
Biểu diễn các điểm trên trên cùng một mặt phẳng tọa độ ta được đồ thị hàm số y = f(x) như sau:
\(C=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=x^{64}-1-x^{64}\)
\(C=-1\)
Vậy gtri của C không phụ thuộc vào x