Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
MC+MB=BC
=>BC=2MB+MB=3MB
=>\(\dfrac{CM}{CB}=\dfrac{2MB}{3MB}=\dfrac{2}{3}\)
Xét ΔCME và ΔCBA có
\(\widehat{CME}=\widehat{CBA}\)(hai góc đồng vị, ME//AB)
\(\widehat{C}\) chung
Do đó: ΔCME đồng dạng với ΔCBA
=>\(\dfrac{CM}{CB}=\dfrac{CE}{CA}=\dfrac{ME}{BA}=\dfrac{2}{3}\)
b: ΔCME đồng dạng với ΔCBA
=>\(\dfrac{C_{CME}}{C_{CBA}}=\dfrac{CM}{CB}=\dfrac{2}{3}\)
=>\(C_{CME}=\dfrac{2}{3}\cdot24=16\left(cm^2\right)\)

a: ΔCEF đồng dạng với ΔCAB theo tỉ số k=CE/CA
ΔADE đồng dạng với ΔABC
=>k'=AD/AB=2/5
b: \(\dfrac{C_{ADE}}{C_{ABC}}=\dfrac{AD}{AB}=\dfrac{2}{5}\)
=>\(C_{ADE}=\dfrac{2}{5}\cdot\left(5+7+9\right)=\dfrac{2}{5}\cdot21=\dfrac{42}{5}\left(cm\right)\)
ΔCEF đồng dạng với ΔCAB
=>\(\dfrac{C_{CEF}}{C_{CAB}}=\dfrac{CE}{CA}=\dfrac{3}{5}\)
=>\(C_{CEF}=\dfrac{3}{5}\cdot\left(5+7+9\right)=\dfrac{3}{5}\cdot21=\dfrac{63}{5}\left(cm\right)\)

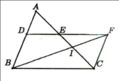
Qua K vẽ đường thẳng // với AB cắt AC tại H.
=> AHKD là hình bình hành => DK = AH (1)
Gọi giao điểm của AK và DH là O. Vì AHKD là HBH => DO = OH
Xét 3 đường thẳng MA, CA, BA đồng quy tại A cắt 2 đường thẳng DH và BC ta được: DO/OH = BM/MC = 1
=> DH // BC (định lí chùm đường thẳng đồng quy đảo)
Xét ∆ ADH và ∆ FEC có:
AD = EF ( t/c đoạn chắn) ; DH = EC (t/c đoạn chắn) ; ^ADH = ^FEC => ∆ ADH = ∆ FEC (c-g-c)
=> AH = CF (2)
Từ (1) và (2) => CF = DK (đpcm)
GL
Do EF//AB⇒\(\frac{CF}{CA}=\frac{EF}{AB}\)⇒\(\frac{CF}{EF}=\frac{AC}{AB}\)(1)
Dựng MG//AC và MM là trung điểm cạnh BC
⇒GM là đường trung bình ΔABC
=⇒G là trung điểm cạnh AB ⇒AG=BG
Do DK//GM⇒\(\frac{AD}{AG}=\frac{DK}{GM}\)⇒\(\frac{AD}{BG}=\frac{DK}{GM}\)
=> \(\frac{DK}{AD}=\frac{GM}{BG}=\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB}\left(2\right)\)
Từ (1) và (2)\(\Rightarrow\frac{CF}{EF}=\frac{DK}{AD}\)
Mà tứ giác ADEF là hình bình hành (vì EF//AD và DE//AF) nên AD=EF
=> CF=DK (đpcm)
Nguồn: thuynga