Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
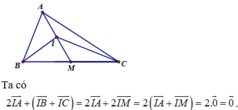
$M$ là trung điểm $BC$ nên $\overrightarrow{BM}, \overrightarrow{CM}$ là 2 vector đối nhau.
$I$ là trung điểm $AM$ nên $-\overrightarrow{IA}=\overrightarrow{IM}$
Từ đây ta có:
$-2\overrightarrow{IA}=2\overrightarrow{IM}=(\overrightarrow{IB}+\overrightarrow{BM})+(\overrightarrow{IC}+\overrightarrow{CM})=\overrightarrow{IB}+\overrightarrow{IC}+(\overrightarrow{BM}+\overrightarrow{CM})$
$=\overrightarrow{IB}+\overrightarrow{IC}$
$\Rightarrow 2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}$
(đpcm)

a: \(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}\)
\(=\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\overrightarrow{BA}-\dfrac{1}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\)

* Xét tam giác IBC có IM là đường trung tuyến nên: 2 I M → = I B → + I C →
Lại có ; I là trung điểm của AM nên I A → + I M → = 0 → ⇒ 2 I A → + 2. I M → = 0 →
Hay I B → + I C → + 2. I M → = 0 →
Đáp án A
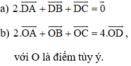


Ta có:
\(\overrightarrow{IB}+\overrightarrow{IC}=2\overrightarrow{IM}\) (1)
Mặt khác: I là trung điểm AM
\(\Rightarrow\overrightarrow{AM}=2\overrightarrow{IM}\) (2)
Từ (1) và (2)
\(\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{AM}\)