Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}x-y=0\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}x-y=0\\2x+y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-1\end{matrix}\right.\)
Tọa độ điểm C là:
\(\left\{{}\begin{matrix}2x+y=-3\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=3\end{matrix}\right.\)
Vậy: A(1;1); B(-1;-1) C(-3;3)
b: \(\overrightarrow{BC}=\left(-2;4\right)=\left(-1;2\right)\)
=>\(\overrightarrow{AH}=\left(2;1\right)\)
=>VTPT của AH là (-1;2)
Phương trình của AH là:
\(-1\left(x-1\right)+2\left(y-1\right)=0\)
=>-x+1+2y-2=0
=>-x+2y-1=0
Tọa độ điểm M là:
\(\left\{{}\begin{matrix}x_M=\dfrac{-1-3}{2}=-2\\y_M=\dfrac{-1+3}{2}=\dfrac{2}{2}=1\end{matrix}\right.\)
Vậy: M(-2;1)
A(1;1) M(-2;1)
\(\overrightarrow{AM}=\left(-3;0\right)\)
=>VTPT là \(\left(0;3\right)\)
PT của AM là:
\(0\cdot\left(x-1\right)+3\left(y-1\right)=0\)
=>3y-3=0

Chọn A.
+ Vì M là trung điểm của BC nên ![]()
Suy ra ![]()
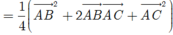
Theo câu trên ta có ![]() nên
nên
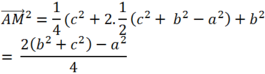

a.
\(\overrightarrow{AB}=\left(4;-2\right)=2\left(2;-1\right)\Rightarrow\) đường thẳng AB nhận (2;-1) là 1 vtcp
Phương trình AB (qua A) có dạng: \(\left\{{}\begin{matrix}x=1+2t\\y=2-t\end{matrix}\right.\)
\(\overrightarrow{CB}=\left(5;-1\right)\Rightarrow\) đường thẳng BC nhận (5;-1) là 1 vtcp
Phương trình BC (qua C) có dạng: \(\left\{{}\begin{matrix}x=5t_1\\y=1-t_1\end{matrix}\right.\)
\(\overrightarrow{CA}=\left(1;1\right)\Rightarrow\) đường thẳng AC nhận (1;1) là 1 vtcp
Phương trình AC (qua A) có dạng: \(\left\{{}\begin{matrix}x=1+t_2\\y=2+t_2\end{matrix}\right.\)
b.
Gọi M là trung điểm BC \(\Rightarrow M\left(\dfrac{5}{2};\dfrac{1}{2}\right)\)
\(\Rightarrow\overrightarrow{AM}=\left(\dfrac{3}{2};-\dfrac{3}{2}\right)=\dfrac{3}{2}\left(1;-1\right)\)
\(\Rightarrow\) Đường thẳng AM nhận (1;-1) là 1 vtcp
Phương trình AM (qua A) có dạng: \(\left\{{}\begin{matrix}x=1+t_3\\y=2-t_3\end{matrix}\right.\)
c.
Đường thẳng AH vuông góc BC nên nhận (1;5) là 1 vtcp
Phương trình AH (qua A) có dạng: \(\left\{{}\begin{matrix}x=1+t_4\\y=2+5t_4\end{matrix}\right.\)
d.
Trung trực AB vuông góc AB nên nhận (1;2) là 1 vtcp
Gọi N là trung điểm AB \(\Rightarrow N\left(3;1\right)\)
Trung trực AB đi qua N và có vtcp là (1;2) nên pt có dạng:
\(\left\{{}\begin{matrix}x=3+t_5\\y=1+2t_5\end{matrix}\right.\)
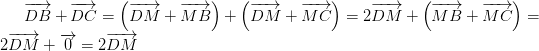
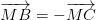
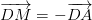
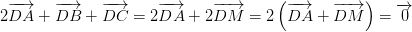
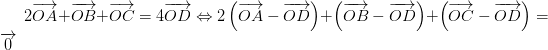
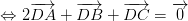 luôn đúng theo câu a
luôn đúng theo câu a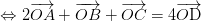 , với O là điểm tùy ý
, với O là điểm tùy ý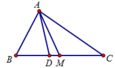
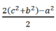
Đáp án B