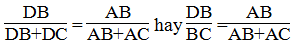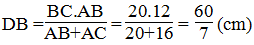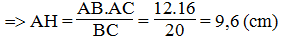Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hiện tai minh chi moi giai được cau a thoi. a, Áp dung định lý py-ta-go cho tam giác Vuông ABC: AB^2+AC^2=BC^2. 6^2+8^2=BC^2 36+64=100. vay can100=10cm
A B C H D
a/ Làm luôn cho hoàn chỉnh:
Xét tam giác ABC vuông tại A có:
\(AB^2+AC^2=BC^2\left(pytago\right)\)
\(6^2+8^2=BC^2\)
\(36+64=BC^2\)
\(100=BC^2\)
\(\Rightarrow BC=\sqrt{100}=10\left(cm\right)\)
b/ Xét tam giác ABC và tam giác AHB có:
\(\hept{\begin{cases}\widehat{ABC}:chung\\\widehat{BAC}=\widehat{AHB}=90^0\left(gt\right)\end{cases}}\)
=> tam giác ABC ~ tam giác HBA (g.g)
c/ Từ chứng minh câu b
\(\Rightarrow\frac{AB}{BH}=\frac{BC}{AB}\Rightarrow AB^2=BC.BH\)
* Tính \(BH\):
Sử dụng chính tỉ số bên trên: \(\frac{AB}{BH}=\frac{BC}{AB}\Leftrightarrow\frac{6}{BH}=\frac{10}{6}\Rightarrow BH=\frac{6.6}{10}=3,6\left(cm\right)\)
* Tính \(HC\):
\(HC=BC-HB=10-3,6=6,4\left(cm\right)\)
d/ Xét tam giác ABD và tam giác ACD có:
\(\hept{\begin{cases}\widehat{BAD}=\widehat{DAC}\left(gt\right)\\\frac{BD}{AB}=\frac{DC}{AC}\left(tinhchatphangiac\right)\end{cases}}\)
=> tam giác ABD ~ tam giác ACD (c.g.c)
Tới đây bí rồi, để nghĩ tiếp

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
Ta có: \(\hat{BAD}+\hat{CAD}=\hat{BAC}=90^0\)
\(\hat{BDA}+\hat{HAD}=90^0\) (ΔHAD vuông tại H)
mà \(\hat{BAD}=\hat{BDA}\) (ΔBAD cân tại B)
nên \(\hat{CAD}=\hat{HAD}\)
=>AD là phân giác của góc HAC
b: Xét ΔAHD và ΔAED có
AH=AE
\(\hat{HAD}=\hat{EAD}\)
AD chung
Do đó: ΔAHD=ΔAED
=>\(\hat{AHD}=\hat{AED}\)
=>\(\hat{AED}=90^0\)
=>ED⊥AC
mà HK⊥AC
nên HK//ED
=>HKED là hình thang
c: ΔAHD=ΔAED
=>DH=DE
=>D nằm trên đường trung trực của HE(1)
Ta có: AH=AE
=>A nằm trên đường trung trực của HE(2)
Từ (1),(2) suy ra AD là đường trung trực của HE
=>AD⊥HE
Xét ΔAEH có
HK,AD là các đường cao
HK cắt AD tại I
Do đó: I là trực tâm của ΔAEH
=>EI⊥AH tại F
mà HC⊥HA
nên EF//HC
=>EFHC là hình thang
Hình thang EFHC có EF⊥FH
nên EFHC là hình thang vuông

45 H B C D a, CM: \(\Delta AHB\)đồng dạng voi\(\Delta CAB\)
- Vì \(AH\perp BC\Rightarrow\widehat{AHB=90^o}\)
- Xét \(\Delta AHB\)và \(\Delta CAB\)có:
\(\widehat{AHB}=\widehat{BAC}\)
\(\widehat{A}\)chung
\(\Rightarrow\Delta AHB\)đồng dạng voi \(\Delta CAB\)(g-g) (đpcm)
b, CM: \(AC^2=CH.BC\)
- Xét \(\Delta AHC\)và \(\Delta BAC\)có:
\(\widehat{AHC}=\widehat{BAC}\left(=90^o\right)\)
\(\widehat{C}\)chung
\(\Rightarrow\Delta AHC\)đòng dạng với\(\Delta BAC\)(g-g)
\(\Rightarrow\frac{AC}{BC}=\frac{HC}{AC}\)
\(\Leftrightarrow AC^2=CH.BC\left(đpcm\right)\)

b) Tam giác ABC vuông tại A có:
\(AB^2+AC^2=BC^2\)(Định lí Py-ta-go)
Thay \(6^2+8^2=BC^2\)
\(36+64=BC^2\)
=> \(BC^2=100\)
=> \(BC=\sqrt{100}=10cm\)
Vì đường trung tuyến Ah ứng với cạnh huyền BC
=> AH = 1/2 BC
=> AH = \(\frac{BC}{2}=\frac{10}{2}=5cm\)
a) Tứ giác AHCD có:
IH=ID(gt); IA=IC(gt)
=> Tứ giác AHCD là hình bình hành (1)
lại có: AH vuông góc với BC(gt)
=> \(\widehat{H}\)= \(^{90^0}\) (2)
Từ (1) và (2) => Tứ giác AHCD là hình chữ nhật

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 122 + 162 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
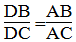
Suy ra:
Suy ra:
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)
b. Ta có: SABC =1/2.AB.AC =1/2.AH.BC
Suy ra: AB.AC = AH.BC
Trong tam giác vuông AHB, ta có: ∠(AHB ) = 90o
Theo định lí Pi-ta-go, ta có: AB2 = AH2 + HB2
Suy ra: HB2 = AB2 - AH2 = 122 - (9,6)2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 607 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠(AHD) = 90o
Theo định lí Pi-ta-go, ta có:
AD2 = AH2 + HD2 = (9,6)2 + (1,37)2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)