

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




B C I H F E A
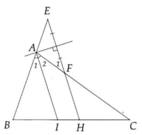
a)Ta có: BAI=CAI (AI là đường phân giác BAC)
Do:FH//AI=>CFH=CAI và BAI=AEF( đồng vị)
Mà:CFH=AFE(2 góc đối đỉnh)
Suy ra: AFE=AEF
Xét \(\Delta\)AFE:AFE=AEF=>\(\Delta\)AFE cân tại A=>Đường trung trực của EF đồng thời là đường cao
Hay:Đường trung trực của EF đi qua A
b) Như đã nói ở câu a:Đường trung trực của EF đồng thời là đường cao, giả sử ấy là AM
Ta có:AMF=90
Mà FH//AI=>AMF+MAI=180=>MAI=90=>AM\(\perp\)AI
Hay đường trung trực của EF vuông góc với AI
c)Do AI cố định nên đường trung trực của EF cố định
Mà \(\Delta\)AFE cân nên đường trung trực của EF đồng thời là đường trung tuyến ứng với EF
Hay đường trung tuyến ứng với EF cố định

a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)

Trong \(\Delta ABC\)cân tại A , ta có :
AH là đường p/g của góc A
\(\Rightarrow\)AH là đường trung trực của BC
OI là đường trung trực của AB
\(\Rightarrow\)O là giao điểm của 3 đường trung trực của \(\Delta ABC\)
=> OC=OA=OB
Xét \(\Delta AOC\)có:
OA=OC ( cmt )
\(\Rightarrow OAC=OCA\)
MÀ \(IAO=OAC\Rightarrow IAO=FCO\)
Xét \(\Delta OEA\)và \(\Delta OFC\)có :
AE= CF ( gt )
EAO=FOC ( cmt )
OA=OC ( cmt )
\(\Rightarrow\Delta OEA=\Delta OFFC\left(c-g-c\right)\)
\(\Rightarrow OE=OF\left(dpcm\right)\)
b, Vì OE=OF ( câu a )
\(\Rightarrow\)O thuộc đường trung trực của EF