Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải
Ta có hình vẽ:
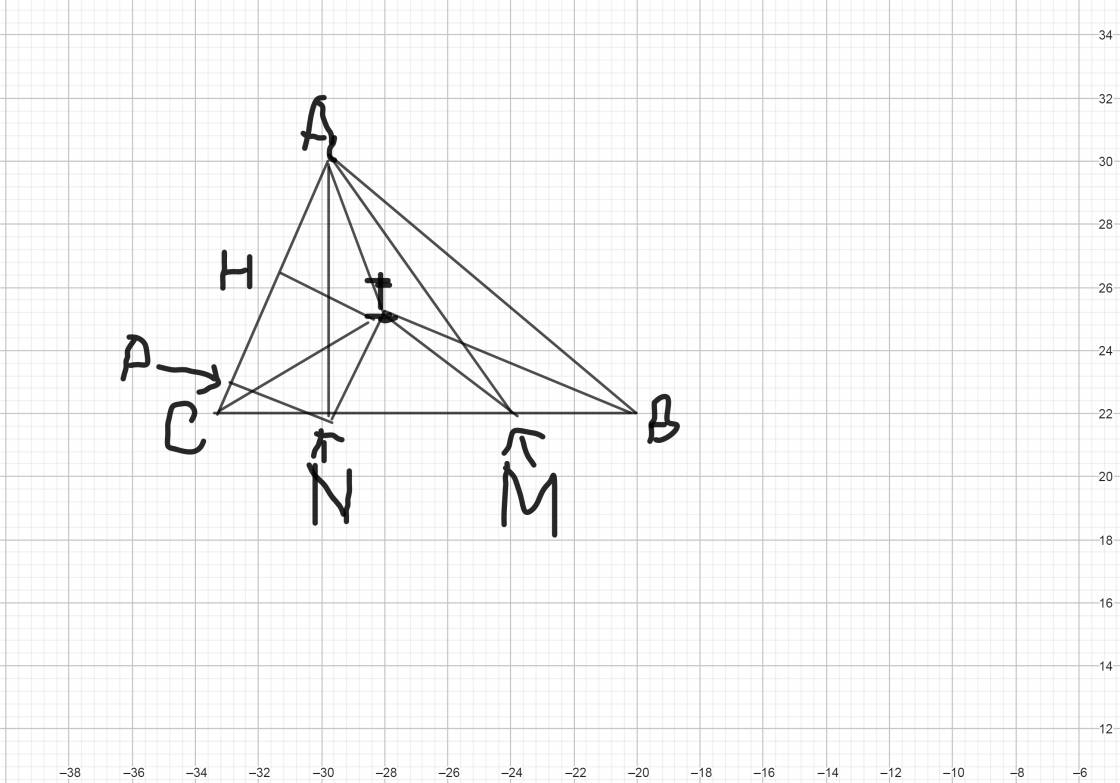
Ta có:
_______________________________
HI=PN(Vì:IM song song AC)
S HTG ACI = AC * HI S HTG ACI= S HTG ANC
2 ______>> Tương tự : S HTG ABI = S HTG AMB
S HTG ANC = AC * PN
2
_________________________________
¼ HTG ABC = S HTG AMB = S HTG ANC
Vì cùng có chiều cao là AN, đáy là ¼ BC nên S HTG ANC = S HTG ABM .
Ta có:
S HTG ANC = S HTG AMB =S HTG ABI = S HTG AMB .
S 1 HTG trong số các hình trên (hay S HTG IAC và IAB) là:
500 : 4 = 125 (cm2)
S HTG IBC là :
500 – (125 * 2) = 250 (cm2)
Đáp số: 125cm2;
250cm2
k giúp mk vs ak

Vì M là trung điểm của cạnh BC nên BM = BC => SABM = SAMC và bằng :
240 : 2 = 120 ( cm2)
Xét hai tam giác IAB và ABM :
- Chung chiều cao hạ từ đỉnh B xuống cạnh AM
- AI = 1/2 AM
=> SAIB = 1/2 x SABM = 120 x 1/2 = 60 ( m2)
Xét hai tam giác IAC và AMC :
- Chung chiều cao hạ từ đỉnh C xuống cạnh AM
- AI = 1/2 AM
=> SAIC = 1/2 x SAMC = 120 x 1/2 = 60 ( cm2)
Vậy diện tích tam giác IBC là :
240 - 60 - 60 = 120 ( cm2)
Đáp số : .....
bsxbjxsjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjssssssssssssssssssssssssssssssssssssjjjjjjjjjjjjjjjjjjjjjjjjjjjjlahã lahjjhahajs

a, - Ta có : \(\left\{{}\begin{matrix}S_{AMD}=\dfrac{1}{2}AM.h\\S_{ADC}=\dfrac{1}{2}AC.h\end{matrix}\right.\)
Mà \(AC=3AM\)
\(\Rightarrow S_{ADC}=3S_{AMD}\)
Lại có : \(\left\{{}\begin{matrix}S_{ABC}=\dfrac{1}{2}BC.h\\S_{ADC}=\dfrac{1}{2}DC.h\end{matrix}\right.\)
Mà \(BC=2DC\)
\(\Rightarrow S_{ABC}=2S_{ADC}=2.3S_{ADM}=6S_{ADM}\)
b, CMTT câu a ta được : \(\left\{{}\begin{matrix}S_{AMN}=\dfrac{1}{6}S_{ABC}\\S_{CMD}=\dfrac{1}{3}S_{ABC}\\S_{BND}=\dfrac{1}{4}S_{ABC}\end{matrix}\right.\)
\(\Rightarrow S_{DMN}=\left(1-\dfrac{1}{6}-\dfrac{1}{3}-\dfrac{1}{4}\right)S_{ABC}=\dfrac{1}{4}S_{ABC}=160\left(cm^2\right)\)