Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tui tick nha
Diện tích tam giác ABN = 1/4 diện tích tam giác ABC vì có chung chiều cao nối từ A xuống N và BN = 1/4 BC
Diện tích tam giác ABN là:
64 x 1/4 = 16 (cm2 )
Diện tích tam giác BMN = 1/2 diện tích tam giác ABN vì có chung chiều cao nối từ N xuống M và BM = 1/2 BA
Diện tích tam giác BMN là:
16 x 1/2 = 8 (cm2 )
Đáp số: 8 cm2

Vì BE=1313× BC mà ABE và ABC chung chiều cao hạ từ A
nên SABESABE=1313 ×=217,5 : 3 = 72,5(cm2)
⇒SADESADE+SBDESBDE=SABESABE \
⇒SADESADE= SABESABE-SBEDSBED
⇒SADESADE =72,5 – 14,55 = 57,95(cm2)
⇒ ADE và ABE chung chiều cao hạ từ E nên SADESABESADESABE=ADABADAB
⇒AB =SADESABESADESABE×AD=72,557,9572,557,95×8=10 (cm)
Cho tam giác ABC có diện tích 240 cm2. Trên BC lấy điểm D sao cho BD=3DC. Tínhdiện tích tam giác ABD. (ĐS cm2) là bài 3. Cho tam giác ABC có diện tích là 400 cm2. Điểm M trên AC sao cho 2xAM=3xCM.Tính diện tích tam giác ABM. (ĐS: cm2) là bài 4. Cho tam giác ABC có diện tích 720 cm2. Trên BC lấy M sao cho BM=1/2 CM. NốiAM , trên AM lấy N sao cho AN=3NM. Tính diện tích tam giác ABN. (ĐS: cm2) là bài 5 nhá các bạn. mình quên cách ra

-Nhìn bài y hệt như bài lớp 8.
-Có: \(AM+MC=AC\) ; \(AM=\dfrac{1}{2}\times MC\Rightarrow MC=2\times AM\)
\(AM+MC=AC\Rightarrow AM+2\times AM=AC\Rightarrow3\times AM=AC\Rightarrow AM=\dfrac{1}{3}\times AC\)
\(\dfrac{S_{APM}}{S_{ABM}}=\dfrac{AP}{AB}=\dfrac{1}{2}\) ; \(\dfrac{S_{ABM}}{S_{ABC}}=\dfrac{AM}{AC}=\dfrac{1}{3}\).
\(\Rightarrow\dfrac{S_{AMN}}{S_{AMB}}\times\dfrac{S_{AMB}}{S_{ABC}}=\dfrac{1}{2}\times\dfrac{1}{3}\)
\(\Rightarrow\dfrac{S_{AMN}}{S_{ABC}}=\dfrac{1}{6}\)
\(\Rightarrow S_{AMN}=\dfrac{1}{6}\times S_{ABC}=\dfrac{1}{6}\times180=30\left(cm^2\right)\).
-Có \(BN+NC=BC\) ; \(BN=NC\) nên \(BN+BN=BC\Rightarrow2\times BN=BC\Rightarrow BN=\dfrac{1}{2}\times BC\)
-Có P là trung điểm của AB nên \(BP=\dfrac{1}{2}\times AB\)
\(\dfrac{S_{BPN}}{S_{BPC}}=\dfrac{BN}{BC}=\dfrac{1}{2}\).
\(\dfrac{S_{BPC}}{S_{ABC}}=\dfrac{BP}{AB}=\dfrac{1}{2}\).
\(\Rightarrow\dfrac{S_{BPN}}{S_{BPC}}\times\dfrac{S_{BPC}}{S_{ABC}}=\dfrac{1}{2}\times\dfrac{1}{2}\)
\(\Rightarrow\dfrac{S_{BPN}}{S_{ABC}}=\dfrac{1}{4}\)
\(\Rightarrow S_{BPN}=\dfrac{1}{4}\times S_{ABC}=\dfrac{1}{4}\times180=45\left(cm^2\right)\)
\(S_{MPNC}=S_{ABC}-S_{APM}-S_{BPN}=180-30-45=105\left(cm^2\right)\)
-Lớp 5 làm gì biết dấu nhân được ẩn trong phép tính \(\dfrac{1}{2}MC\) ?

Chọn điểm N trên BC và giả sử S_MCN=S_AMNB.
Nối AN.
Do AM=1/4AC hay AM=1/3MC
Ta có: S_MNC=3S_AMN (MC=3AM, chung đường cao từ N)
Để S_AMNB=SMNC thì S_ANB=(3-1)S_AMN=2S_AMN
Diện tích ABC có 3+1+2=6 (phần) thì S_ANB có 2 phần hay S_ANB=1/3S_ABC.
Suy ra: BN=1/3BC
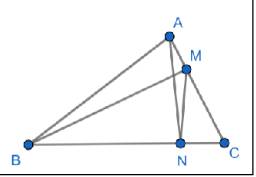


\(AM=\dfrac{1}{3}AC\) nên \(CM=\dfrac{2}{3}CA\)
=>\(S_{CMB}=\dfrac{2}{3}\cdot S_{CAB}=\dfrac{2}{3}\cdot54=36\left(cm^2\right)\)
Vì CN=1/4 CB nên \(S_{CNM}=\dfrac{1}{4}\cdot S_{CMB}=\dfrac{1}{4}\cdot36=9\left(cm^2\right)\)
\(S_{AMNB}+S_{CNM}=S_{ABC}\)
=>\(S_{AMNB}=54-9=45\left(cm^2\right)\)