Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



B C A
Có \(\Delta ABC~\Delta DEF\)
\(\Rightarrow\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}\)
Ta có cạnh nhỏ nhất của \(\Delta ABC\)là 6 cm mà cạnh nhỏ nhất của \(\Delta DEF\)là 9 cm
vậy \(\Rightarrow DE=9cm\)
Độ dài cạnh DE là : \(\frac{AB}{DE}=\frac{AC}{DF}\Leftrightarrow\frac{6}{9}=\frac{14}{DF}\)
\(\Rightarrow DF=\frac{14.9}{6}=21cm\)
Độ dài cạnh EF là : \(\frac{AB}{DE}=\frac{AC}{DF}\Leftrightarrow\frac{6}{9}=\frac{10}{EF}\)
\(\Rightarrow EF=\frac{10.9}{6}=15cm\)
Chúc bạn học tốt !

Bài làm
Gọi độ dài của DF là x
Độ dài của EF là y
Vì tam giác ABC ~ Tam giác DEF
=>
hay
Vậy DF = 21 ( cm )
EF = 15 ( cm )
# Vô thống kê của mik xem hình #

Ta có: ΔABC∼ΔDEF
nên AB/DE=BC/EF=AC/DF
=>6/9=10/EF=14/DF
=>10/EF=14/DF=2/3
=>EF=15cm; DF=21cm

6.)
Khi 2 tam giác đồng dạng với nhau thì cạnh nhỏ nhất của tam giác này sẽ tương ứng với cạnh nhỏ nhất của tam giác kia.
Theo đề:\(A'B'\)=4,5
Ta có:\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
\(\Rightarrow\)\(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow\)\(B'C'=7,5cm,C'A'=10,5cm\)

ΔABC đồng dạng với ΔDEF
=>AB/DE=BC/EF=AC/DF
=>4/DE=6/EF=8/DF
=>2/DE=3/EF=4/DF=9/9=1
=>DE=2cm; EF=3cm; DF=4cm

Bài 7:
Đặt a=A'B',b=A'C', c=B'C'
Theo đề,ta có: a/6=b/8=c/10
mà cạnh nhỏ nhất trong tam giác A'B'C' là 9cm
nên b/8=c/10=9/6=3/2
=>b=12cm; c=15cm

Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất bằng 4,5 nên cạnh nhỏ nhất của △ A'B'C' tương ứng với cạnh AB nhỏ nhất của △ ABC
Giả sử A'B' là cạnh nhỏ nhất 'của Δ A'B'C'
Vì
△
A'B'C' đồng dạng
△
ABC nên 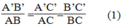
Thay AB = 3(cm), AC = 7(cm), BC = 5(cm), A'B' = 4,5(cm) vào (1) ta có: 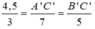
Vậy: