Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

Đáp án D
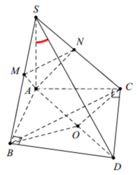
Gọi O là tâm đường tròn ngoại tiếp Δ A B C , D là điểm đối xứng với A qua O.
⇒ O A = O B = O D suy ra tam giác ABD vuồn tại B ⇒ A B ⊥ B D .
Ta có A B ⊥ B D S A ⊥ B D ⇒ B D ⊥ S A B ⇒ B D ⊥ A M suy ra A M ⊥ S B D .
Suy ra A M ⊥ S D . Tương tự, ta chứng minh được A N ⊥ S D
Do đó S D ⊥ A M N . suy ra A B C ; A M N ^ = S A ; S D ^ = A S D ^
Tam giác SAD vuông tại A, có tan A S D ^ = A D S A
Mà đường kính A D = 2 x R Δ A B C = B C sin 120 ∘ = 3 2 x S A
Vậy tan A S D ^ = 3 3 ⇒ A S D ^ = 30 ∘ ⇒ A B C ; A M N ^ = 30 ∘

Đáp án D
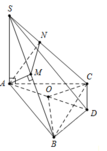
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Và D là điểm đối xứng với A qua O.


a) Ta có: góc FAB + góc BAC = 90 độ
góc EAC + góc BAC = 90 độ
=> Góc FAB = góc EAC
AF=AC; AB=AE
=> Tam giác AFB = tam giác ACE
=> FB=EC
b) Lấy K sao cho M là trung điểm của AK thì ta có ACKB là hình bình hành nên góc ACB =180* - góc BAC. Ta cũng tính dc góc FAE= 180* - góc BAC ( tổng của BAC với 2 lần góc CAE, mà góc CAE=90* -góc BAC). Thêm với AC=AF , CK=AE (=AB) nên tam giác ACK = tam giác FAE nên AK=EF mà AK=2AM nên EF=2AM
c) Gọi H là giao của AM và EF. Tam giác ACK = tam giác FAE nên góc CAK = góc AFE, mà góc CAK phụ với góc MAF nên góc AFE cũng phụ góc MAF. Xét trong tam giác AHF có góc F và góc A phụ nhau nên tam giác AHF vuông tại H suy ra AM vuông góc với EF.
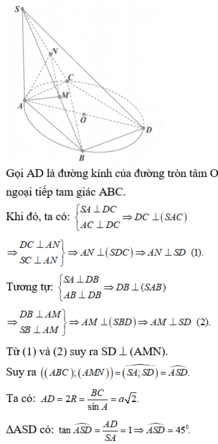




Chọn B.
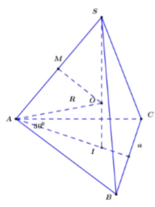
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, và D là điểm đối xứng với A qua O.
Ta có BD ⊥ AB (góc nội tiếp chắn nửa đường tròn).
Và BD ⊥ SA ⇒ BD ⊥ ( SAB ) ⇒ BD ⊥ AM .
Mặt khác AM ⊥ SB ⇒ AM ⊥ ( SBD ) ⇒ SD ⊥ AM .
Chứng minh tương tự ta được SD ⊥ AN ⇒ SD ⊥ ( AMN ) .
Ta có SD ⊥ ( AMN ) SA ⊥ ( ABC ) ⇒ ( ( AMN ) ; ( ABC ) ^ )
= ( SA ; SD ^ ) = ASD ^ .
Ta có: AD = 2 R ABC = BC sin A ^ = a 2
Vậy ( ( AMN ) ; ( ABC ) ^ ) = ASD ^ = arctan 1 = 45 o