Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tam giác ABC có BC^2=52^2=2704
mà AB^2+AC^2=20^2+48^2=2704
=> BC^2=AB^2+AC^2
=> tam giác ABC vuông tại A
b) tam giác ABC vuông tại A=> AH.BC=AB.AC
=> AH.52=20.48
=> AH.52=960
=> AH=240/13cm

sao chứng minh được \(\Delta ABC\)cân tại \(A\) khi đề bài cho \(AB=20\)và \(AC=48\)
\(\Delta\)cân là 2 cạnh bên của nó phải bằng nhau
đọc đề mình đã thấy nó không hợp lí rồi Nguyễn Hải Văn

bài 1 : AH = \(\sqrt{119}\)cm
bài 2 : BN = \(\sqrt{49.54}\)cm
* hình tự vẽ
1/
Xét tam giác ABC: tam giác ABC là tam giác cân(gt) mà AH là đường cao(vì AH\(\perp\)BC)=> AH cũng là đường trung tuyến=> BH=HC
Ta có: BC=HB+HC, mà HB=HC(cmt)=> HB=HC=\(\frac{BC}{2}\)=> HB=HC= 5cm
Xét tam giác ACH, theo định lý Py ta go, có:
AH^2+ HC^2=AC^2
=> AH^2+ 5^2= 12^2
=> AH^2= 144-25
=> AH^2= 119=> AH= căn 119cm
2/ Xét tam giác BCA, theo định lý Py ta go, có:
BA^2+ AC^2= BC^2=> 12^2+5^2=BC^2
=> 144+25= BC^2=> BC^2= 169=>BC=13cm
Mà M là trung điểm BC(gt)=> MB=MC nên ta có BC=MB+MC=> MB=MC=\(\frac{BC}{2}\)=> MB=MC=6,5
Xét tam giác BMN, theo định lý Py ta go, có:
BN^2+NM^2= BM^2
=> BN^2+2,7^2=6,5^2=> BN^2 = 42,25-7,29=> BM^2= 34,96=> BM= căn 34,96cm
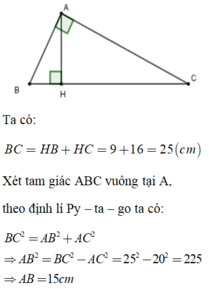

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{240}{13}\left(cm\right)\)