Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N
Do M, N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC nên MN//BC.
Do vậy hai véc tơ \(\overrightarrow{NM}\) và \(\overrightarrow{BC}\) cùng phương.

A B C M N K
Theo các xác định điểm M, N ta có:
\(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB};\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}.\)
Theo tính chất trung điểm của MN ta có:
\(\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\).


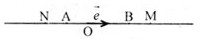
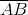 = 3;
= 3; 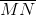 = -5. Từ đây ta có
= -5. Từ đây ta có 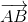 = 3
= 3 ,
, 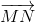 = -5
= -5
Lời giải:
Với $M$ là trung điểm của $AB$, $N$ là trung điểm của $AC$ thì $MN$ là đường trung bình của tam giác $ABC$
Do đó \(\overrightarrow {MN}=\frac{1}{2}\overrightarrow {BC}\)
Mà \(B(9;7);C(11;-1)\Rightarrow \overrightarrow {BC}=(2;-8)\)
\(\Rightarrow \overrightarrow{MN}=\frac{1}{2}\overrightarrow{BC}=(1;-4)\)