Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
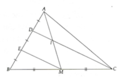

A B C M I D K
Vẽ K là trung điểm CD
Ta có KM là đường trung bình của tam giác CBD
\(\Rightarrow MK=\frac{1}{2}BD=AD\) và MK//AD
Do đó ADMKM là hình bình hành
\(\Rightarrow I\)là trung điểm của DK\(\Rightarrow DI=\frac{1}{2}DK\)
Mà \(DK=\frac{1}{2}CD\)
Vậy DI=\(\frac{1}{4}CD\)

A B C M D I E
Đề sửa lại 1 chỗ: AD = 1/3 AC
Bài làm:
Gọi E là trung điểm của DC
=> EM là đường TB của tam giác BDC
=> EM // BD => EM // ID
Lại có: AD = 1/3 AC => AD = 1/2 DC = DE
=> D là trung điểm của AE, mà ID // ME
=> I là trung điểm AM => AI = IM
=> đpcm