Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

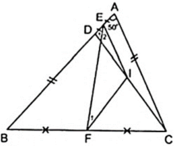
Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác ACD và BCD.
Đặt BD = AC = 2a
Áp dụng định lý đường trung bình của hai tam giác trên ta có:
( 1 ) FI//BD ( 2 ) FI = a
( 3 ) EI = a ( 4 ) EI//AC


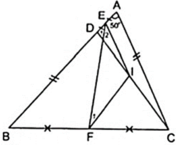
Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác BCD và ACD.
Đặt BD = AC = 2a
Áp dụng định lý đường trung bình của hai tam giác trên ta có:
( 1 ) FI//BD ( 2 ) FI = a
( 3 ) EI = a ( 4 ) EI//AC


A B C M N D I
Nối C với D. Gọi I là trung điểm CD. Nối I với M và N.
Xét \(\Delta\)CAD: M là trung điểm AD; I là trung điểm CD => IM là đường trung bình của \(\Delta\)CAD
=> IM = AC/2 (1)
Tương tự: IN là đường trung bình của \(\Delta\)CBD => IN = DB/2 (2)
Từ (1) và (2) => IM =IN => \(\Delta\)MIN cân ở I => ^IMN = ^INM.
Lại có: IN là đường trung bình \(\Delta\)CBD => IN // BD hay IN // BM => ^INM = ^BMN (So le trg)
=> ^IMN = ^BMN = 1/2 ^BMI.
Mặt khác: IM là đường trung bình \(\Delta\)CAD => IM // AC => ^BMI = ^BAC (Đồng vị)
=> ^BMN = 1/2. ^BAC hay ^BAC = 2.^BMN (đpcm).