Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác BKC và tam giác CHB
+ BC chung
+ BK = HC vì AB = AC ; AK = AH => AB-AK=AC-AH
+ góc ABC = góc HCB (tam giác ABC cân)
Vậy tam giác BKC = tam giác CHB (c.g.c)
Và góc BKC = góc CHB
\(\widehat{KOB}=\widehat{HOC}\)(đối đỉnh)
\(\widehat{BKO}=\widehat{CHO}\left(cmt\right)\)
\(\Rightarrow\widehat{KBO}=\widehat{HCO}\)(3 góc trong tam giác)
Xét \(\Delta OKB\)và \(\Delta OHC\)
+ BK = HC
+ \(\widehat{KBO}=\widehat{OCH}\)
+ \(\widehat{OKB}=\widehat{OHC}\)
Vậy \(\Delta OKB=\Delta OHC\left(g.c.g\right)\)
VÀ OH = OK (hai cạnh tương ứng ) => Tam giác OKH cân tại O
OB = OC (hai cạnh tương ứng) => Tam giác OBC cân tại O
c) Xét \(\Delta AKO\)và \(\Delta AHO\)
+ AO chung
+ OK = OH
+ AH = AK
\(\Rightarrow\Delta AKO=\Delta AHO\left(c.c.c\right)\)
=> Góc KAO = góc HAO
Gọi giao điểm của KH và AO là F
Xét tam giác AFK và tam giác AFH
+ AK = AH
+ ÀF chung
+góc KAF = góc HAF (cmt)
Vậy tam giác AFK = tam giác AFH (c.g.c)
Và KF = FH(hai cạnh tương ứng)
Hay AO đi qua trung điểm của HK

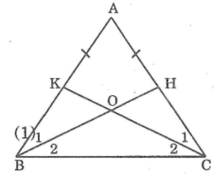
Hình vẽ:
A B C K H O 1 2 1 2
Giải:
Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(AH=AK\left(gt\right)\)
\(\widehat{A}\) là góc chung
\(AB=AC\) ( Vì \(\Delta ABC\) cân tại \(A\) )
Do đó: \(\Delta ABH=\Delta ACK\left(c.g.c\right)\)
\(\Rightarrow\widehat{B_2}=\widehat{C_2}\) ( cặp góc tương ứng )
Mà \(\widehat{B}=\widehat{C}\) ( Do \(\Delta ABC\) cân tại \(A\) )
\(\Rightarrow\widehat{B}-\widehat{B_2}=\widehat{C}-\widehat{C_2}\)
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)
\(\Rightarrow\Delta OBC\) cân tại \(O\) . \(\left(đpcm\right)\)

+) Xét ΔABH và ΔACK, ta có:
AB = AC ( vì tam giác ABC cân tại A)
AH = AK (giả thiết)
Suy ra: ΔABH = ΔACK(c.g.c)

+ Do đó, tam giác OBC cân tại O.

a) Vì tam giác ABC cân => \(\hept{\begin{cases}AB=AC\\\widehat{ABM}=\widehat{ANC}\end{cases}}\)
mà BM=CN => \(\Delta AMB=\Delta ANC\left(cgc\right)\)=> AM=AN
=> Tam giác AMN cân tại A
b) \(S_{AMB}=S_{ANC}\)=> \(BH\cdot AM=CK\cdot AN\)
<=> BH=CK (vì AM=AN)
c) \(\hept{\begin{cases}\widehat{AHB}=\widehat{AKC}=90^o\\AB=AC\\BH=CK\end{cases}\Rightarrow\Delta AHB=\Delta AKC\left(ch-gv\right)}\)
=> AH=CK
Lời giải:
a) Xét tam giác $ABH$ và $ACK$ có:
\(AB=AC\) (gt)
\(\widehat{A}\) chung
\(AK=AH\) (gt)
\(\Rightarrow \triangle ABH=\triangle ACK(c.g.c)\Rightarrow BH=CK\)
b)
Vì \(AB=AC; AK=AH\Rightarrow AB-AK=AC-AH\Rightarrow BK=CH\)
Từ tam giác bằng nhau phần a suy ra:
\(\widehat{ABH}=\widehat{ACK}\Leftrightarrow \widehat{KBO}=\widehat{HCO}\)
\(\widehat{AHB}=\widehat{AKC}\Rightarrow 180^0-\widehat{AHB}=180^0-\widehat{AKC}\)
\(\Rightarrow \widehat{CHO}=\widehat{BKO}\)
Xét tam giác $OKB$ và $OHC$ có:
\(KB=HC\) (cmt)
\(\widehat{OBK}=\widehat{OCH}\) (cmt)
\(\widehat{BKO}=\widehat{CHO}\) (cmt)
\(\Rightarrow \triangle OKB=\triangle OHC\) (g.c.g) (đpcm)
\(\Rightarrow OB=OC\)
c)
Xét tam giác $AOB$ và $AOC$ có:
\(\left\{\begin{matrix} OB=OC(cmt)\\ \text{OA chung}\\ AB=AC\end{matrix}\right.\Rightarrow \triangle AOB=\triangle AOC(c.c.c)\)
\(\widehat{OAB}=\widehat{OAC}\Rightarrow OA\) là phân giác góc $\widehat{BAC}$
Hình vẽ:
