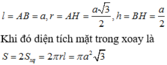Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chứng minh được AH=BH -> SA= SB _> tam giác SAB cân ở S
gọi M là trung điểm của AB -> SM vuông góc với AB -> góc giữa mp (SAB) và mp (ABC) là góc SMH -> góc SMH = 60 độ
-> tìm được SH -> tìm được thể tích
tìm diên tích tam giác SAB -> khoảng cách từ C đến mp (SAB)
Vì I là trung điểm của SC nên khoảng cách từ I đến mp (SAB) bằng một nửa khoảng cách từ C đến mp (SAB)

2 đường thẳng thì cắt nhau tại 1 điểm
n đường thẳng sẽ cắt nhau tại \(C^{n_{ }}_2\) điểm ( tổ hợp nhé)
vậy 4 đường sẽ có \(C^4_2\)= 6 điểm

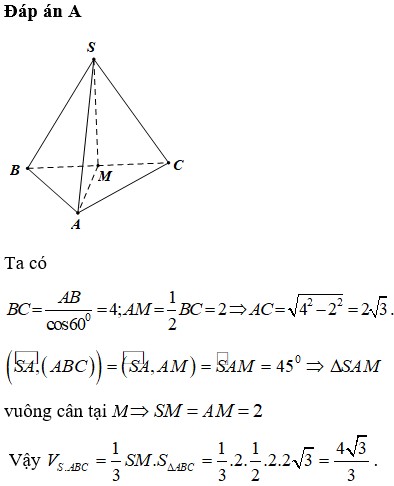
Lời giải:
\(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CS}{CF}=4\Leftrightarrow \frac{DM}{AD}+\frac{EN}{BE}+\frac{FS}{CF}=1\)
\(\Leftrightarrow \frac{HD}{AD}+\frac{EH}{BE}+\frac{HF}{CF}=1\) \((\star)\)
Gọi diện tích của các tam giác \(AFH, BFH, BHD, DHC, EHC, AEH\) lần lượt là \(a,b,c,d,e,f\)
Ta có :
\(\left\{\begin{matrix} \frac{DH}{AD}=\frac{S_{BHD}}{S_{BAD}}=\frac{S_{CHD}}{S_{ADC}}\\ \frac{EH}{BE}=\frac{S_{AEH}}{S_{ABE}}=\frac{S_{CHE}}{S_{EBC}}\\ \frac{HF}{CF}=\frac{S_{BFH}}{S_{BFC}}=\frac{S_{FAH}}{S_{FAC}}\end{matrix}\right.\)\(\Leftrightarrow \left\{\begin{matrix} \frac{DH}{AD}=\frac{c}{a+b+c}=\frac{d}{e+f+d}=\frac{c+d}{a+b+c+d+e+f}\\ \frac{EH}{BE}=\frac{f}{a+b+f}=\frac{e}{e+c+d}=\frac{e+f}{a+b+c+d+e+f}\\ \frac{HF}{CF}=\frac{b}{b+c+d}=\frac{a}{a+f+e}=\frac{a+b}{a+b+c+d+e+f}\end{matrix}\right.\)
\(\Rightarrow \frac{DH}{AD}+\frac{EH}{BE}+\frac{HF}{CF}=1\)
Ta có \((\star)\) nên phép cm hoàn tất.

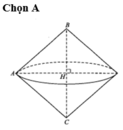
Tam giác ABC quay quanh trục là đường thẳng BC tạo ra hai hình nón.
-Hình nón đỉnh B, đường sinh BA.
-Hình nón đỉnh C, đường sinh CA.
Xét hình nón đỉnh B ta có: