Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

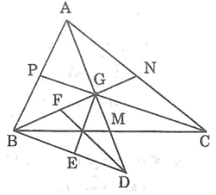
a. Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.
Ta có: AG = GD (gt)
AG = 2GM (tính chất đường trung tuyến)
Suy ra: GD = 2GM
Mà GD = GM + MD ⇒ GM = MD
Xét ΔBMD và ΔCMG, ta có:
BM = CM (gt)
∠(BMD) = ∠(CMG) (đối đỉnh)
MD = GM (chứng minh trên)
Suy ra: ΔBMD = ΔCMG (c.g.c)
⇒ BD = CG (hai cạnh tương ứng)
Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)
Suy ra: BD = 2/3 CP (1)
Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)
Và AG = 2/3 AM (tính chất đường trung tuyến)
Suy ra: GD = 2/3 AM (3)
Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.
b. Ta có: GM = MD (chứng minh trên)
Suy ra BM là đường trung tuyến của tam giác BGD.
Suy ra: BM = 1/2 BC (4)
Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:
FG = 1/2 BG (tính chất đường trung tuyến)
GN = 1/2 GB (tính chất đường trung tuyến)
Suy ra: FG = GN
Xét ΔDFG và ΔANG, ta có:
AG = GD (gt)
∠(DGF) = ∠(AGN) (đối đỉnh)
GF = GN (chứng minh trên)
Suy ra: ΔDFG = ΔANG (c.g.c) ⇒ DF = AN
Mà AN = 1/2 AC (gt)
Suy ra: DF = 1/2 AC (5)
Mặt khác: BD = CG (chứng minh trên)
ED = 1/2 BD (vì E là trung điểm BD)
GP = 1/2 CG (tính chất đường trung tuyến)
Suy ra: ED = GP
Lại có: ΔBMD = ΔCMG (chứng minh trên)
⇒ ∠(BDM) = ∠(CGM) hay ∠(EDG) = ∠(CGM)
(CGM) = (PGA) (đối đỉnh)
Suy ra: ∠(EDG) = ∠(PGA)
AG = GD (gt)
Suy ra: ΔPGA = ΔEDG (c.g.c) ⇒ GE = AP mà AP = 1/2 AB (gt)
Do đó: GE = 1/2 AB(6)
Từ (4), (5) và (6) suy ra các đường trung tuyến của ΔBGD bằng một nửa cạnh của ΔABC.

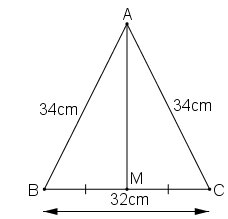
a. Xét ΔAMB và ΔAMC, ta có:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
b. Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).

Cái bài này mình đã từng đăng để hỏi mấy bạn kia.
Nhưng đề câu này thiểu bạn ơi.
Phải có x=a/m ; y=b/m
À thôi, mk viết đầy đủ đề thử nhé !
Giả sử:x=a/m;y=b/m (a,b,m thuộc Z.m > 0) và x < y.
Hãy chứng minh (chứng tỏ) rằng nếu chọn z=a+b/2m thì ta có x < y < z.
Trong sách lớp 7 đề y như z đó !
Mk ghi cách làm luôn nha !
Giả sử x=a/m,y=b/m (a,b,m thuộc Z,m > 0 )
Vì x < y nên ta suy ra a < b.
ta có: x=a/m, y=b/m <=> x=2a/am. y=2b/2m
mà a < b nên a+a < a+b <=> 2a < a+b
Do 2a < a+b thì x < y ( 1 )
Ta lại có: a < b nên a+b < b+b <=> a+b < 2b
Mà a+b < 2b <=> x < z ( 2 )
Từ ( 1 ) và ( 2 ) suy ra x < y < z (ĐPCM)

TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt


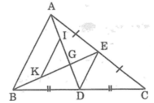
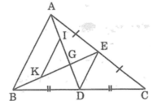
Vì AD và BE là 2 đường trung tuyến của ΔABC cắt nhau tại G nên theo tính chất đường trung tuyến, ta có: AG = 2/3 AD

Áp dụng kết quả bài 64 chương II sách Bài tập toán 7 vào ΔABC và ΔAGB ta có:
DE // AB và DE = 1/2 AB (1)
IK // AB và IK = 1/2 AB (2)
Từ (1) và (2) suy ra:
DE // IK và DE = IK.
 (a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 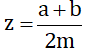 thì ta có x < z < y.
thì ta có x < z < y.
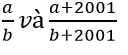

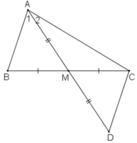
Trên tia đối tia MA lấy điểm D sao cho MD = MA
Xét ΔAMB và ΔDMC, ta có:
MA = MD (theo cách vẽ)
∠(AMB) = ∠(DMC) (đối đỉnh)
MB = MC (gt)
Suy ra: ΔAMB = ΔDMC (c.g.c)
Suy ra: AB = CD (2 cạnh tương ứng)
và ∠D = ∠A1(2 góc tương ứng) (1)
Mà AB < AC (gt)
nên: CD < AC
Trong ΔADC, ta có: CD < AC
Suy ra: ∠D > ∠A2(đối diện cạnh lớn hơn là góc lớn hơn) (2)
Từ (1) và (2) suy ra: ∠A1 > ∠A2hay ∠(BAM) > ∠(MAC) .