Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1)
a) trong tam giac ABC vuong tai A co
+)BC2=AB2+AC2
suy ra AC=12cm
+)AH.BC=AB.AC
suy ra AH=7,2cm
b) Trong tu giac AMHN co HMA=HNA=BAC=90 do suy ra AMHN la hcn suy ra AH=MN=7,2cm
suy ra MN=7,2cm
c) goi O la giao diem cu MN va AH
Vi AMHN la hcn (cmt) nen OA=OH=7,2/2=3,6cm
suy ra SBMCN=1/2[OH*(MN+BC)]=39,96cm2
d) Vi AMHN la hcn nen goc AMN=goc HAB
Trong tam giac ABC vuong tai A co AK la dg trung tuyen ung voi canh huyen BC nen AK=BK=KC
suy ra tam giac AKB can tai K
suy ra goc B= goc BAK
Ta co goc B+ goc BAH=90 do
tuong duong BAK+AMN=90 do suy ra AK vuong goc voi MN (dmcm)
a, \(vì\)AD là phân giác suy ra góc BAD =góc DAC =45 ĐỘ
cos45 độ = AD/AB =4 /AB =1/ căn 2 suy ra AB =4 NHÂN CĂN 2
TH TỰ dùng sin 45 độ =dc/ac =5/ad =1/căn 2 suy ra AC =5 CĂN 2 ÁP DỤNG PITA GO TÌM RA CẠNH bc
b,
bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)
a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
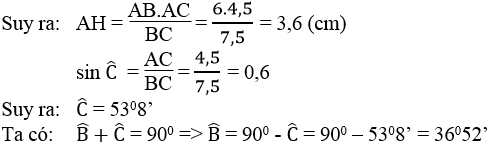b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
Giải tam giác nhé em, ta vần vận dụng định lý Pitago và các hệ thức lượng.
Áp dụng đl Pitago ta có: \(BC=\sqrt{AB^2+AC^2}=5\)
Áp dụng hệ thức lượng \(BH=\frac{AB^2}{BC}=1,8\Rightarrow CH=BC-BH=3,2\)
\(AH=\sqrt{BH.CH}=2,4\)
\(sinB=\frac{AC}{BC}=0,8\Rightarrow B\approx53^08'\Rightarrow C\approx36^052'\)
Ta có: \(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\)
Ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}\left(cm\right)\)
Ta có: \(AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{4^2}{5}=\dfrac{16}{5}\left(cm\right)\)
Lời giải:
Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=BC-BH=5-1,8=3,2$ (cm)
Nếu BC2 = AC2 + AB2 thì tam giác ABC vuông tại A. (Pytago)
ta có: 7,52 = 4,52 + 62 => tam giác ABC vuông tại A.
Tam giác ABC vuông tại A, đường cao AH nên: AH.BC = AC.AB <=> AH = (AC.AB)/BC <=> AH = 3,6 cm
Ta có: AB2 = BC.BH <=> BH = AB2 /BC <=> 36/7,5 = 4,8 cm
=> HC = BC - BH = 7.5 - 4.8 = 2.7 cm
a) Ta có: \(AB^2+AC^2=3^2+4^2=25\)
Và \(BC^2=5^2=25\)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại \(A\)(định lí Pytago đảo)
b) \(\Delta ABC\) vuông tại \(A\)có: \(AB.AC=AH.BC\) (hệ thức về cạnh và đường cao trong tam giác vuông)
\(\Rightarrow AH=\frac{AB.AC}{BC}\)
\(\Rightarrow AH=\frac{3.4}{5}=\frac{12}{5}\left(cm\right)\)
a,Xét tam giác ABC có : AB^2 +AC^2 =BC^2
Tương đương : BC^2 : 3^2 +4^2 =25
suy ra : BC=5
Vậy tam giác ABC vương tại A
b,Ta có : ABC là tam giác vuông tại A . Suy ra AB.AC=AH. BC. Suy ra AH = (AB.AC) /BC. AH=(3.4) /5=12/5 (cm)