Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\overrightarrow{BC}=\left(4;1\right)\)
Đường cao kẻ từ A vuông góc BC nên nhận (4;1) là 1 vtpt
Phương trình đường cao:
\(4\left(x-1\right)+1\left(y-4\right)=0\Leftrightarrow4x+y-8=0\)
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2)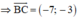 
Phương trình đường cao AH đi qua A(2;-1) nhận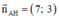 
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.
1.2
a.
\(\overrightarrow{AB}=\left(4;-2\right)=2\left(2;-1\right)\Rightarrow\) đường thẳng AB nhận (1;2) là 1 vtpt
Phương trình đường thẳng AB:
\(1\left(x+1\right)+2\left(y-4\right)=0\Leftrightarrow x+2y-7=0\)
b.
Gọi M là trung điểm AB \(\Rightarrow M\left(1;3\right)\)
\(AB=\sqrt{4^2+\left(-2\right)^2}=2\sqrt{5}\) \(\Rightarrow AM=\dfrac{1}{2}AB=\sqrt{5}\)
Đường tròn đường kính AB có tâm M và bán kính \(R=AM=\sqrt{5}\) nên có pt:
\(\left(x-1\right)^2+\left(y-3\right)^2=5\)
1.1
a. \(\overrightarrow{CB}=\left(5;15\right)=5\left(1;3\right)\) ; \(\overrightarrow{CA}=\left(7;11\right)\)
Đường cao qua A vuông góc BC nên nhận (1;3) là 1 vtpt
Phương trình đường cao đi qua A có dạng:
\(1\left(x-4\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-13=0\)
Đường cao qua B vuông góc AC nhận (7;11) là 1 vtpt có dạng
\(7\left(x-2\right)+11\left(y-7\right)=0\Leftrightarrow7x+11y-91=0\)
Trực tâm H là giao điểm 2 đường cao nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+3y-13=0\\7x+11y-91=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=13\\y=0\end{matrix}\right.\)
\(\Rightarrow H\left(13;0\right)\)
Đáp án: C
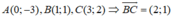
Đường cao kẻ từ A của tam giác ABC là đường thẳng đi qua A và nhận vecto BC là vecto pháp tuyến
⇒ d: 2(x - 0) + (y + 3) = 0 ⇔ 2x + y + 3 = 0
Đường cao AH là đường thẳng đi qua A(1; 4) và vuông góc với BC.
= (3; 3) =>
⊥
nên
nhận vectơ
= (3; 3) làm vectơ pháp tuyến và có phương trình tổng quát:
AH : 3(x – 1) + 3(y -4) = 0
3x + 3y – 15 = 0
=> x + y – 5 = 0
Gọi M là trung điểm BC ta có M (;
)
Trung tuyến AM là đường thẳng đi qua hai điểm A, M. Theo các viết phương trình đường thẳng đi qua hai điểm trong câu a) ta viết được:
AM : x + y – 5 = 0
Đáp án B
AH là đường cao của tam giác nên đường thẳng này đi qua A( 2; -1) và nhận C B → ( 7 ; 3 ) làm VTPT .
Suy ra; phương trình đường cao AH là:
7(x- 2) +3( y+1) = 0 hay 7x+ 3y -11= 0
Ta có : \(\overrightarrow{BC}=\left(4;1\right)\)
Phương trình đường cao của \(\Delta ABC\) kẻ từ A : \(4\left(x-1\right)+1\left(y-4\right)=0\Leftrightarrow4x+y-8=0\)