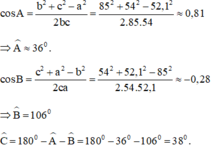Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.

+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
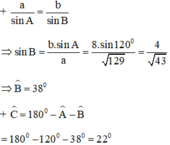

Gọi H là giao điểm của BM và CN. Ta có:
Diện tích tam giác ABC = 1/2 * AB * AC = 1/2 * 8 cm * 12 cm = 48 cm^2
Theo định lí Menelaus, ta có:
(BH/HA) * (AN/NC) * (CM/MB) = 1
Thay giá trị vào ta được:
(BH/HA) * (4/8) * (5/7) = 1
Suy ra: BH/HA = 14/15
Do đó, AH = AB - BH = 8 cm - (14/15)*8 cm = 8/15 cm
Tương tự, ta có: CH = 12/15 cm
Áp dụng công thức diện tích tam giác bằng nửa tích chất của đường cao, ta có:
Diện tích tam giác AMN = 1/2 * AM * NH = 1/2 * (AB - BM) * AH = 1/2 * (8 cm - 5 cm) * 8/15 cm = 8/15 cm^2
Vậy diện tích hình tam giác AMN là 8/15 cm^2.

a) Xét tổng a2 + b2 – c2 = 82 + 102 – 132 = -5 < 0
Vậy tam giác này có góc C tù
cos C = =
≈ -0, 3125 =>
= 91047’
b) Áp dụng công thức tính đường trung tuyến, ta tính được AM ≈ 10,89cm

a: \(\cos A=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{10^2+13^2-8^2}{2\cdot10\cdot13}=\dfrac{205}{2\cdot10\cdot13}>0\)
=>góc A nhọn
\(\cos C=\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{8^2+10^2-13^2}{2\cdot8\cdot10}=-\dfrac{5}{2\cdot8\cdot10}< 0\)
=>góc C tù
=>ΔABC tù
b: \(MA^2=\dfrac{2\left(b^2+c^2\right)-a^2}{4}=\dfrac{2\cdot\left(10^2+13^2\right)-8^2}{4}=118.5\left(cm\right)\)
nên \(MA=\dfrac{\sqrt{474}}{2}\left(cm\right)\)

a)\(2\overrightarrow{OA}+\overrightarrow{DB}+\overrightarrow{DC}\)
\(=2\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{DB}+\overrightarrow{DO}+\overrightarrow{DC}\)
\(=2\overrightarrow{OA}-2\overrightarrow{OA}=\overrightarrow{O}\)(ĐPCM)
b) \(20\overrightarrow{A}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(=2\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{OB}+\overrightarrow{DC}-\overrightarrow{DO}\)
\(=20\overrightarrow{A}-20\overrightarrow{A}+4\overrightarrow{OD}=4\overrightarrow{OD}\)(ĐPCM)